


基本的例題(II)
物理学基礎論 A
運動の法則
第 6 講 (平成 19 年 5 月 15 日)
(基本的例題)
今回から二回に渡って、幾つかの基本的例題を通じて運動方程式の解法の
具体的な方法を示す。一般に、運動方程式の解法は次の4つのステップから
なる。
- (1)
- 物体に働く力を全て探し出す。
- (2)
- 運動方程式をたてる。
- (3)
- 一般解を求める。
- (4)
- 初期条件から題意に即した解を得る。
1. 放物運動
水平方向に 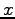 -軸、
-軸、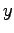 -軸、垂直方向に
-軸、垂直方向に 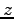 -軸をとり、
それぞれの方向への単位ベクトルを
-軸をとり、
それぞれの方向への単位ベクトルを
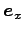 ,
,
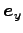 ,
,
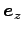 とする。
とする。
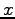 -
-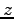 平面内で仰角
平面内で仰角 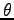 の方向に大きさ
の方向に大きさ 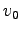 の速度で
打ち上げた玉 (質量
の速度で
打ち上げた玉 (質量 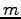 とする) の水平面での到達距離を求める。
座標系
とする) の水平面での到達距離を求める。
座標系
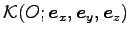 は絶対静止座標系で慣性系で
あると仮定する。すなわち、地球の自転等の効果は無視する。
は絶対静止座標系で慣性系で
あると仮定する。すなわち、地球の自転等の効果は無視する。
(1) 玉に働く力は、
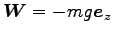 (重力)
(重力)
(2) 運動方程式は
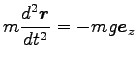 |
|
|
(0) |
そこで、
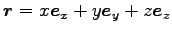 として、各成分で書くと
として、各成分で書くと
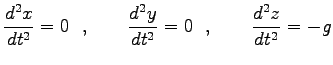 |
|
|
(0) |
(3) 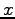 ,
, 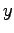 方向は等速運動、
方向は等速運動、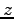 方向は自由落下運動である。
積分は簡単に出来て
方向は自由落下運動である。
積分は簡単に出来て
| |
|
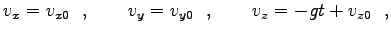 |
|
| |
|
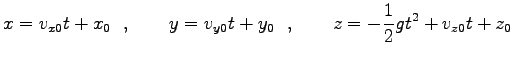 |
(0) |
と一般解が求まる。ここに、
 等は
積分定数である。
等は
積分定数である。
(4) 初期条件として、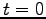 で
で 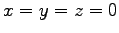 ,
,
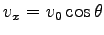 ,
,
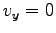 ,
,
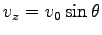 をとると、積分定数が決まり
をとると、積分定数が決まり
| |
|
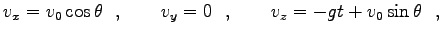 |
|
| |
|
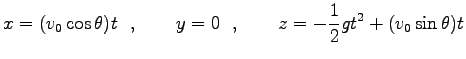 |
(0) |
と解が求まる。これを、
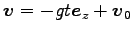 ,
,
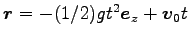 とベクトルに
まとめて書くと便利である。ここに
とベクトルに
まとめて書くと便利である。ここに
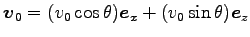 である。
である。
運動の軌跡は、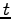 を
を 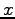 の函数として表わし、それを
の函数として表わし、それを 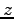 の式に
入れることにより
の式に
入れることにより
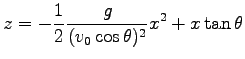 |
|
|
(0) |
これは放物線である。最高点に達するまでの時間は 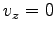 とする
ことにより、
とする
ことにより、
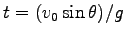 .
これを、
.
これを、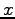 と
と 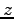 の式に代入することにより、最高点の座標が求まる。
また、着地点までの距離は、
の式に代入することにより、最高点の座標が求まる。
また、着地点までの距離は、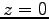 を
を 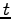 について解くことにより、
着地点までの時間が
について解くことにより、
着地点までの時間が
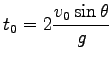 |
|
|
(0) |
と求まるので、これを 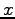 の式に代入して
の式に代入して
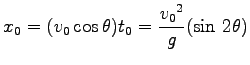 |
|
|
(0) |
と求まる。Eq. (4.6) の 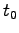 は最高点に達するまでの時間の丁度 2 倍である。
特に、
は最高点に達するまでの時間の丁度 2 倍である。
特に、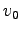 =一定、の条件のもとに一番遠くまで玉を飛ばすことの
出来る角度は、
=一定、の条件のもとに一番遠くまで玉を飛ばすことの
出来る角度は、
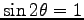 , つまり
, つまり
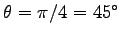 の
角度で投げ上げた場合である。
の
角度で投げ上げた場合である。
(大気の抵抗を考慮した場合)
この時、最大の到達距離を得るためには、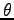 を
を 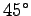 より
大きくすればよいか、あるいは小くすればよいかという問題を
考えてみる。経験によれば、一般に大気の抵抗力は速度に比例して
その向きに逆の方向をもつ。これを、
より
大きくすればよいか、あるいは小くすればよいかという問題を
考えてみる。経験によれば、一般に大気の抵抗力は速度に比例して
その向きに逆の方向をもつ。これを、
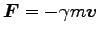 (
( は定数) とすると、Eq. (4.1) の運動方程式は
は定数) とすると、Eq. (4.1) の運動方程式は
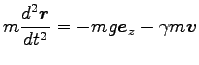 |
|
|
(0) |
と変更をうける。加速度を
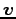 で書くと
で書くと
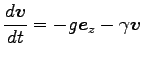 |
|
|
(0) |
そこで、
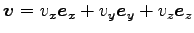 として
として
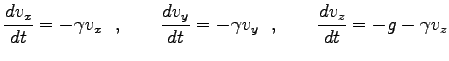 |
|
|
(0) |
という 3 つの独立した微分方程式が得られる。まず 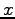 方向の成分の解は
方向の成分の解は
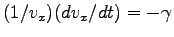 として
として 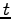 で積分することにより、
で積分することにより、
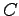 を積分定数として、
を積分定数として、
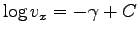 である。
そこで
である。
そこで 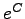 を新しく
を新しく  とおくと
とおくと
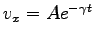 と
求まる。同様に、
と
求まる。同様に、 方向の積分は
方向の積分は
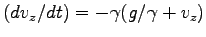 を
を
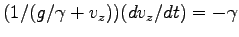 と書いて
と書いて 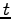 で積分
することにより
で積分
することにより
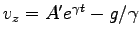 である。ここに
である。ここに
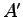 は新しい積分定数である。結局、速度の一般解は
は新しい積分定数である。結局、速度の一般解は
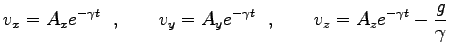 |
|
|
(0) |
ここに、積分定数 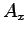 ,
, 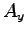 ,
, 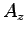 は
は 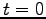 で
で
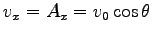 ,
,  ,
,
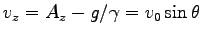 であることにより、
であることにより、
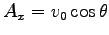 ,
, 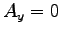 ,
,
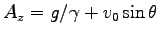 と求まる。結局、速度の解は
と求まる。結局、速度の解は
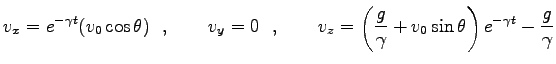 |
|
|
(0) |
これを、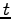 でもう 1 度積分して
でもう 1 度積分して
ここに、新しい積分定数 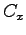 ,
, 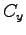 ,
, 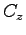 は
は 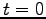 で
で
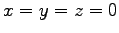 であることから決まる。結局、最終的な解として
であることから決まる。結局、最終的な解として
が求まる。
運動の軌跡の式は、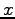 の式から
の式から 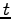 を
を 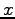 で表して、これを
で表して、これを 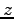 の
式に代入すれば求められるが、今の場合、あまり簡単な式にはならない。
それよりも重要なのは、
の
式に代入すれば求められるが、今の場合、あまり簡単な式にはならない。
それよりも重要なのは、
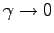 の極限で、以前の
空気抵抗の無い場合の式になるか、ということである。
これを見るために、指数函数
の極限で、以前の
空気抵抗の無い場合の式になるか、ということである。
これを見るために、指数函数 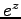 の Taylor 展開
の Taylor 展開
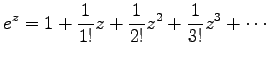 |
|
|
(0) |
を利用する。これを用いると
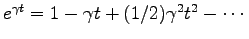 より、
より、
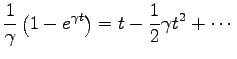 |
|
|
(0) |
となるので、これを Eq. (4.14) に代入すると
となり、
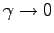 の時 Eq. (4.4) に帰着する。
Eq. (4.17) で、
の時 Eq. (4.4) に帰着する。
Eq. (4.17) で、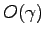 は
は 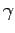 の 1 次の order の微少量で
あることを示す。
また、
の 1 次の order の微少量で
あることを示す。
また、
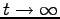 の極限で Eq. (4.12) は
の極限で Eq. (4.12) は
となる。ここで、最後の 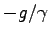 は、もとの式 Eq. (4.10) で
は、もとの式 Eq. (4.10) で
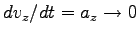 となった時の極限の速度に対応しており、
これを空気抵抗のある時の''終端速度''と呼んでいる。
また、
となった時の極限の速度に対応しており、
これを空気抵抗のある時の''終端速度''と呼んでいる。
また、
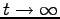 の時 Eq. (4.14) から
の時 Eq. (4.14) から
であることにより、
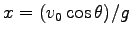 は
は 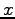 -
-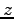 平面上での
軌跡の漸近線であることがわかる。
平面上での
軌跡の漸近線であることがわかる。
今度は、反対の極限として 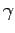 が十分大きい時を考える。
Eq. (4.10) からすぐ分かるように、
が十分大きい時を考える。
Eq. (4.10) からすぐ分かるように、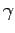 は [1/s] の次元を
もっているので、いま考えている問題に特徴的な時間
は [1/s] の次元を
もっているので、いま考えている問題に特徴的な時間 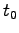 を
考えて、
を
考えて、
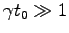 の場合を考えることになる。
の場合を考えることになる。
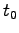 として、ここでは玉が再び地表に達するまでの時間、
すなわち
として、ここでは玉が再び地表に達するまでの時間、
すなわち 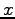 -
-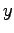 平面 (
平面 (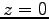 平面) への到達時間を考えることにする。
この時、Eq. (4.14) で
平面) への到達時間を考えることにする。
この時、Eq. (4.14) で
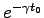 を無視すると
を無視すると
となる。ここに、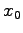 は
は 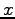 -
-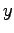 平面での到達距離である。下の式より
平面での到達距離である。下の式より
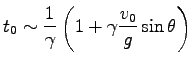 |
|
|
(0) |
が得られるので、これを
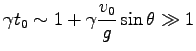 |
|
|
(0) |
と書くと、今考えている条件
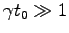 より、
Eq. (4.22) の右辺の 1 はその後の
より、
Eq. (4.22) の右辺の 1 はその後の
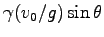 に
比べて無視できることがわかる。そこで
に
比べて無視できることがわかる。そこで
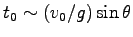 . これは、大気の抵抗が無い場合の式
Eq. (4.6) と同じ order の時間である。
Eq. (4.20) の上の式からは、到達距離
. これは、大気の抵抗が無い場合の式
Eq. (4.6) と同じ order の時間である。
Eq. (4.20) の上の式からは、到達距離 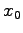 は
は 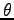 が
小さい方が有利であることがわかる。しかし、
が
小さい方が有利であることがわかる。しかし、
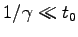 を
用いると、
を
用いると、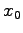 は
は
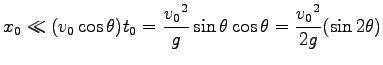 |
|
|
(0) |
より、抵抗がない場合よりも常に小さいことがわかる。
実際は、 はかなり大きい。
仮に、
はかなり大きい。
仮に、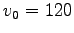 km/s とすると、
km/s とすると、
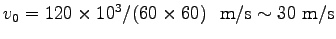 だから、
だから、
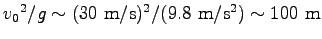 . そこで、
. そこで、
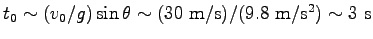 . ここに、
. ここに、
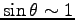 とした。
そこで、もし
とした。
そこで、もし
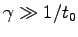 なら、
なら、
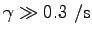 となる。
となる。
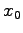 は
は 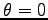 の時最大だが、
の時最大だが、
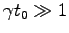 を満すためには
ある程度の角度は必要である。以上より、大気の抵抗がある場合に
一定の初速度のもとに最大の到達距離を得るためには、
を満すためには
ある程度の角度は必要である。以上より、大気の抵抗がある場合に
一定の初速度のもとに最大の到達距離を得るためには、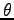 を
を 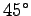 より
は小くとる方がよいことが予想される。
より
は小くとる方がよいことが予想される。



基本的例題(II)
物理学基礎論 A
運動の法則
Yoshikazu Fujiwara
平成19年5月16日
![]() -軸、
-軸、![]() -軸、垂直方向に
-軸、垂直方向に ![]() -軸をとり、
それぞれの方向への単位ベクトルを
-軸をとり、
それぞれの方向への単位ベクトルを
![]() ,
,
![]() ,
,
![]() とする。
とする。
![]() -
-![]() 平面内で仰角
平面内で仰角 ![]() の方向に大きさ
の方向に大きさ ![]() の速度で
打ち上げた玉 (質量
の速度で
打ち上げた玉 (質量 ![]() とする) の水平面での到達距離を求める。
座標系
とする) の水平面での到達距離を求める。
座標系
![]() は絶対静止座標系で慣性系で
あると仮定する。すなわち、地球の自転等の効果は無視する。
は絶対静止座標系で慣性系で
あると仮定する。すなわち、地球の自転等の効果は無視する。
![]() (重力)
(重力)
![]() ,
, ![]() 方向は等速運動、
方向は等速運動、![]() 方向は自由落下運動である。
積分は簡単に出来て
方向は自由落下運動である。
積分は簡単に出来て
![]() で
で ![]() ,
,
![]() ,
,
![]() ,
,
![]() をとると、積分定数が決まり
をとると、積分定数が決まり
![]() を
を ![]() の函数として表わし、それを
の函数として表わし、それを ![]() の式に
入れることにより
の式に
入れることにより
![]() を
を ![]() より
大きくすればよいか、あるいは小くすればよいかという問題を
考えてみる。経験によれば、一般に大気の抵抗力は速度に比例して
その向きに逆の方向をもつ。これを、
より
大きくすればよいか、あるいは小くすればよいかという問題を
考えてみる。経験によれば、一般に大気の抵抗力は速度に比例して
その向きに逆の方向をもつ。これを、
![]() (
(![]() は定数) とすると、Eq. (4.1) の運動方程式は
は定数) とすると、Eq. (4.1) の運動方程式は
![]() の式から
の式から ![]() を
を ![]() で表して、これを
で表して、これを ![]() の
式に代入すれば求められるが、今の場合、あまり簡単な式にはならない。
それよりも重要なのは、
の
式に代入すれば求められるが、今の場合、あまり簡単な式にはならない。
それよりも重要なのは、
![]() の極限で、以前の
空気抵抗の無い場合の式になるか、ということである。
これを見るために、指数函数
の極限で、以前の
空気抵抗の無い場合の式になるか、ということである。
これを見るために、指数函数 ![]() の Taylor 展開
の Taylor 展開
![]() が十分大きい時を考える。
Eq. (4.10) からすぐ分かるように、
が十分大きい時を考える。
Eq. (4.10) からすぐ分かるように、![]() は [1/s] の次元を
もっているので、いま考えている問題に特徴的な時間
は [1/s] の次元を
もっているので、いま考えている問題に特徴的な時間 ![]() を
考えて、
を
考えて、
![]() の場合を考えることになる。
の場合を考えることになる。
![]() として、ここでは玉が再び地表に達するまでの時間、
すなわち
として、ここでは玉が再び地表に達するまでの時間、
すなわち ![]() -
-![]() 平面 (
平面 (![]() 平面) への到達時間を考えることにする。
この時、Eq. (4.14) で
平面) への到達時間を考えることにする。
この時、Eq. (4.14) で
![]() を無視すると
を無視すると