


: 質点系の運動
物理学基礎論 A
>保存力と中心力
第 10 講 (平成 19 年 6 月 19 日)
5.3 角運動量と力のモーメント
或る点 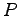 にベクトル
にベクトル
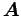 が与えられた時、また別の点
が与えられた時、また別の点 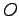 のまわりの
ベクトル
のまわりの
ベクトル
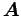 のモーメントを
のモーメントを
![$\displaystyle [({\boldsymbol r}_P-{\boldsymbol r}_O)\times {\boldsymbol A}]$](img4.png) |
|
|
(0) |
で定義する。位置ベクトル
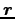 にある質点の運動量
にある質点の運動量
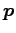 のモーメント
のモーメント
![$\displaystyle {\boldsymbol M}=[({\boldsymbol r}-{\boldsymbol r}_O)\times {\boldsymbol p}]$](img7.png) |
|
|
(0) |
を、この質点の点 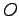 のまわりの角運動量という。この質点に力
のまわりの角運動量という。この質点に力
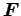 が働く時、
が働く時、
![$\displaystyle {\boldsymbol N}=[({\boldsymbol r}-{\boldsymbol r}_O)\times {\boldsymbol F}]$](img9.png) |
|
|
(0) |
を、点 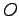 のまわりの力のモーメントという。
のまわりの力のモーメントという。
以下、簡単のため 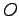 を座標原点にとり、''原点のまわりの'' を省略する。
(しかし、''どのまわりの'' かは重要である。)
を座標原点にとり、''原点のまわりの'' を省略する。
(しかし、''どのまわりの'' かは重要である。)
(1 質点の運動)
より (
![$ [{\boldsymbol v}\times {\boldsymbol v}]=0$](img14.png) に注意)
に注意)
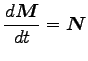 |
|
|
(0) |
(この式は、
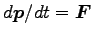 に類似している。)
特に、
に類似している。)
特に、
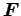 が
が
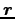 と平行 (中心力) なら、
と平行 (中心力) なら、
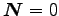 より
より
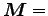 一定、である。これを、「角運動量の保存則」という。
一定、である。これを、「角運動量の保存則」という。
(幾何学的意味)
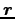 と
と
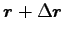 で囲まれる扇形の部分の面積は近似的に
で囲まれる扇形の部分の面積は近似的に
![$\displaystyle \Delta S=\frac{1}{2}\vert[{\boldsymbol r}\times \Delta {\boldsymb...
...}{2}\vert[{\boldsymbol r}\times ({\boldsymbol v}\Delta t)]\vert+O((\Delta t)^2)$](img20.png) |
|
|
(0) |
で表される。ここで、
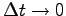 の極限をとって
の極限をとって
![$\displaystyle \frac{d S}{dt}=\lim_{\Delta t \rightarrow 0} \frac{\Delta S}{\Del...
...(\Delta t)\right)
=\frac{1}{2}\vert[{\boldsymbol r}\times {\boldsymbol v}]\vert$](img22.png) |
|
|
(0) |
そこで
![$\displaystyle \vert{\boldsymbol M}\vert=\vert[{\boldsymbol r}\times {\boldsymbol p}]\vert
=m\vert[{\boldsymbol r}\times {\boldsymbol v}]\vert=2m \frac{dS}{dt}$](img23.png) |
|
|
(0) |
つまり、角運動量の大きさは面積速度 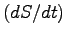 に比例する。
一般に、''角運動量は、質点の運動平面に垂直で、
その大きさは面積速度に比例する。'' 角運動量の運動方程式 Eq. (5.70)
は、力のモーメントが角運動量を変化させることを意味する。
に比例する。
一般に、''角運動量は、質点の運動平面に垂直で、
その大きさは面積速度に比例する。'' 角運動量の運動方程式 Eq. (5.70)
は、力のモーメントが角運動量を変化させることを意味する。



: 質点系の運動
物理学基礎論 A
>保存力と中心力
Yoshikazu Fujiwara
平成19年6月26日
![]() にベクトル
にベクトル
![]() が与えられた時、また別の点
が与えられた時、また別の点 ![]() のまわりの
ベクトル
のまわりの
ベクトル
![]() のモーメントを
のモーメントを
![]() を座標原点にとり、''原点のまわりの'' を省略する。
(しかし、''どのまわりの'' かは重要である。)
を座標原点にとり、''原点のまわりの'' を省略する。
(しかし、''どのまわりの'' かは重要である。)
![]() と
と
![]() で囲まれる扇形の部分の面積は近似的に
で囲まれる扇形の部分の面積は近似的に