


: 中心力による運動
: 物理学基礎論 A
: 角運動量と力のモーメント
質点系とは、質量 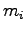 (
(
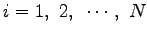 ) をもつ質点の集りである。
ここでは、質点系の運動方程式や種々の保存則について調べる。
) をもつ質点の集りである。
ここでは、質点系の運動方程式や種々の保存則について調べる。
6.1 重心系と実験室系
質点系の各質点間に働く力を内力といい、外界から働く力を外力という。
内力には作用・反作用の法則が成り立つ。
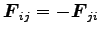 各質点の運動量を
各質点の運動量を
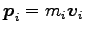 とすると、運動方程式は (慣性系で)
とすると、運動方程式は (慣性系で)
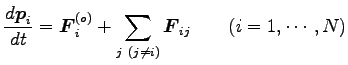 |
|
|
(0) |
質点系の全運動量
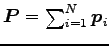 は
は
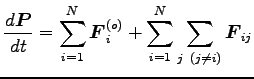 |
|
|
(0) |
を満す。ここに、内力の和は
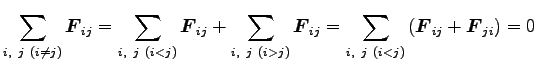 |
|
|
(0) |
より
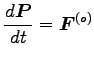 |
|
|
(0) |
ここに
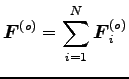 |
|
|
(0) |
は、外力の和である。もし、質点系に働く外力の和がゼロの場合 (あるいは、
外力が全く働かない孤立系ならば)、
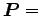 一定。
すなわち、全運動量は保存する。
一定。
すなわち、全運動量は保存する。
(重心系)
重心 (質量中心: center of mass)
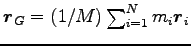 (ここに、
(ここに、
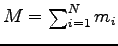 は質点系の全質量) が座標原点にある座標系
を重心系という。そのような座標系での位置ベクトルは
は質点系の全質量) が座標原点にある座標系
を重心系という。そのような座標系での位置ベクトルは
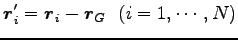 |
|
|
(0) |
であり、それは重心からみた位置ベクトルである。実際、重心系での重心は
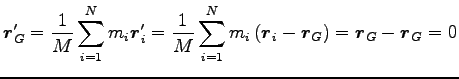 |
|
|
(0) |
である。また、重心系での各質点の速度は、
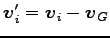 である。
ここに
である。
ここに
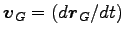 は、重心の速度である。
重心系での全運動量は
は、重心の速度である。
重心系での全運動量は
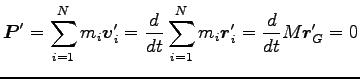 |
|
|
(0) |
一方
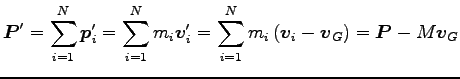 |
|
|
(0) |
より、Eq. (6.8) とあわせて
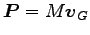 |
|
|
(0) |
つまり、もとの座標系 (実験室系という) での全運動量は、
重心に全質量が集まったとみなした時の重心運動の運動量に等しい。
また、重心系とは全運動量がゼロの系であるとも言える。
(例: 2 体衝突問題)
外界から遮断された 2 質点系の全質量を 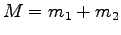 とする。
まず、外力が働かないから、全運動量は保存される。
とする。
まず、外力が働かないから、全運動量は保存される。
ここに、
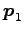 ,
,
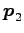 は衝突前の 2 質点の運動量、
は衝突前の 2 質点の運動量、
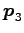 ,
,
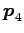 は衝突後の 2 質点の運動量である。
そこで、
は衝突後の 2 質点の運動量である。
そこで、
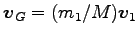 を重心の速度、重心を
を重心の速度、重心を
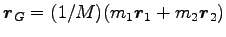 として
として
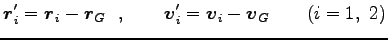 |
|
|
(0) |
また、重心系での粒子 1, 2 の運動量は、衝突前の相対速度を
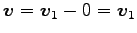 として
として
ここに
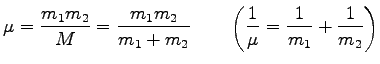 |
|
|
(0) |
を 2 質点系の換算質量という。重心系での全運動量
は
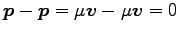 である。
ついでに、衝突前の全運動エネルギーは
である。
ついでに、衝突前の全運動エネルギーは
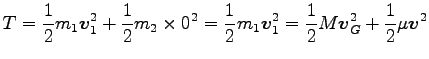 |
|
|
(0) |
である。実際
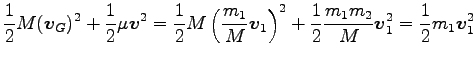 |
|
|
(0) |
Eq. (6.15) で、
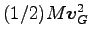 は重心運動の運動エネルギー、
は重心運動の運動エネルギー、
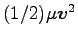 は重心系での (相対運動の) 運動エネルギーである。
実際
は重心系での (相対運動の) 運動エネルギーである。
実際
第 11 講 (平成 19 年 6 月 26 日)
6.2 質点系の角運動量
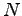 個の質点系を考え、
個の質点系を考え、
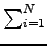 を簡単のため
を簡単のため 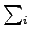 と書く。
質点系の全角運動量は
と書く。
質点系の全角運動量は
![$\displaystyle {\boldsymbol M}=\sum_i {\boldsymbol M}_i=\sum_i [{\boldsymbol r}_...
...mes {\boldsymbol p}_i]
=\sum_i m_i [{\boldsymbol r}_i \times {\boldsymbol v}_i]$](img76.png) |
|
|
(0) |
これを、時間 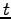 で微分し、Eq. (6.1) を用いると
で微分し、Eq. (6.1) を用いると
作用・反作用の法則により
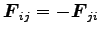 だから
だから
内力が中心力の時 (2 点 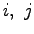 に働く力が、その質点を結ぶ方向を向く時)、
上はゼロ。そこで
に働く力が、その質点を結ぶ方向を向く時)、
上はゼロ。そこで
![$\displaystyle \frac{d {\boldsymbol M}}{dt}=\sum_i [{\boldsymbol r}_i \times {\boldsymbol F}^{(0)}_i]$](img85.png) |
|
|
(0) |
特に、孤立系 (外力=0) の時
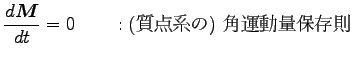 |
|
|
(0) |
(重心運動の分離)
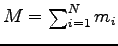 かつ
かつ
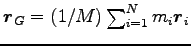 (系の重心)
として、Eq. (6.6) の相対座標を用いると、
(系の重心)
として、Eq. (6.6) の相対座標を用いると、
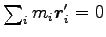 より
より
ここに、
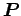 は Eq. (6.10) の質点系の全運動量である。そこで
は Eq. (6.10) の質点系の全運動量である。そこで
と分解される。ここに、内部角運動量は系の重心のまわりの角運動量である。
実際、
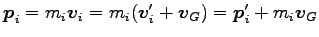 より
より
![$\displaystyle \sum_i [({\boldsymbol r}_i-{\boldsymbol r}_G) \times {\boldsymbol...
...\boldsymbol r}^\prime_i \times {\boldsymbol p}^\prime_i]={\boldsymbol M}^\prime$](img100.png) |
|
|
(0) |
外力のモーメントも
ここに、
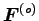 は Eq. (6.5) の外力の総和である。そこで
は Eq. (6.5) の外力の総和である。そこで
![$\displaystyle {\boldsymbol N}^{(o)\prime}=\sum_i \left[{\boldsymbol r}_i \times {\boldsymbol F}^{(o)}_i \right]
\qquad : \hbox{重心系での外力のモーメント}$](img105.png) |
|
|
(0) |
とすると
![$\displaystyle {\boldsymbol N}^{(o)}={\boldsymbol N}^{(o)\prime}+\left[{\boldsymbol r}_G \times {\boldsymbol F}^{(o)} \right]$](img106.png) |
|
|
(0) |
そこで、内力が中心力だとすると
![$\displaystyle \frac{d}{dt} \left( {\boldsymbol M}^\prime+{\boldsymbol M}_G\righ...
...mbol N}^{(o)\prime}+\left[{\boldsymbol r}_G \times {\boldsymbol F}^{(o)}\right]$](img107.png) |
|
|
(0) |
だが
![$\displaystyle \frac{d}{dt}{\boldsymbol M}_G=\left[{\boldsymbol r}_G \times \fra...
...ol P}}{dt} \right]
=\left[{\boldsymbol r}_G \times {\boldsymbol F}^{(o)}\right]$](img108.png) |
|
|
(0) |
より、
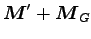 の時間変化は
の時間変化は
![$\displaystyle \frac{d}{dt} {\boldsymbol M}^\prime={\boldsymbol N}^{(o)\prime} ...
...} {\boldsymbol M}_G=\left[{\boldsymbol r}_G \times {\boldsymbol F}^{(o)}\right]$](img110.png) |
|
|
(0) |
と分解される。特に、孤立系では、
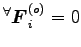 より
より
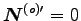 ,
,
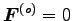 から
から
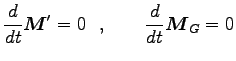 |
|
|
(0) |
つまり、重心の角運動量も内部角運動量も独立に保存される。
(内力を中心力と仮定)
(例 : 万有引力により引きあう 2 質点系)
運動方程式は
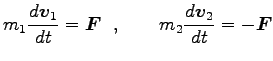 |
|
|
(0) |
ここに
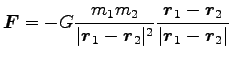 |
|
|
(0) |
相対位置ベクトルを
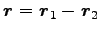 とすると、
とすると、
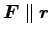 より
万有引力は中心力である。 2 質点系は、内力が中心力で、かつ外力が働かないから、
より
万有引力は中心力である。 2 質点系は、内力が中心力で、かつ外力が働かないから、
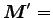 一定、かつ
一定、かつ
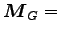 一定。重心系での位置ベクトルは
一定。重心系での位置ベクトルは
そこで、それぞれ 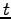 で微分して
で微分して 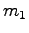 ,
, 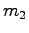 をかけると
をかけると
ここに、
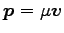 (
(
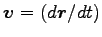 : 相対速度) は相対
運動量であり、
: 相対速度) は相対
運動量であり、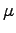 は Eq. (6.14) で定義した換算質量である。
(重心系での全運動量はゼロ:
は Eq. (6.14) で定義した換算質量である。
(重心系での全運動量はゼロ:
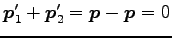 )
内部角運動量
)
内部角運動量
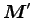 は
は
であり、これは重心系での角運動量であって、相対運動の角運動量とも
よばれる。また、もとの運動方程式 Eq. (6.33) から
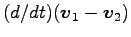 を
作ると、容易に
を
作ると、容易に
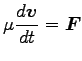 |
|
|
(0) |
が示せる。つまり、Eq. (6.33) の 2 体問題は、Eq. (6.38) で
表される「換算質量 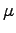 の 1 体問題に帰着される。」
相対運動量は
の 1 体問題に帰着される。」
相対運動量は
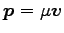 、相対運動の角運動量
は
、相対運動の角運動量
は
![$ {\boldsymbol M}^\prime=[{\boldsymbol r}\times {\boldsymbol p}]$](img140.png) である。
である。
6.3 質点系のエネルギー
もとの運動方程式 Eq. (6.1) と
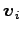 との内積をとり、
との内積をとり、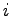 で
和をとると
で
和をとると
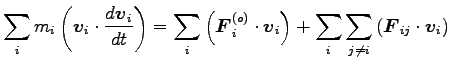 |
|
|
(0) |
ここに、左辺
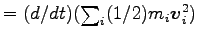 .
また、作用・反作用の法則により
.
また、作用・反作用の法則により
そこで、
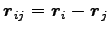 とすると、Eq. (6.39) の
右辺第 2 項は
とすると、Eq. (6.39) の
右辺第 2 項は
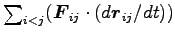 と
表される。従って
と
表される。従って
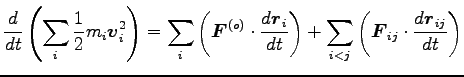 |
|
|
(0) |
これを、
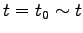 まで積分すると
まで積分すると
| |
|
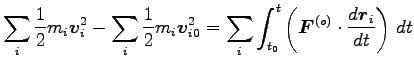 |
|
| |
|
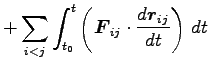 |
(0) |
そこで
として
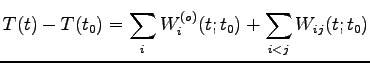 |
|
|
(0) |
まず、内力
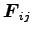 が相対ベクトル
が相対ベクトル
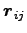 だけの函数で、かつ
保存力であるとすると、任意の閉じた経路に対
して
だけの函数で、かつ
保存力であるとすると、任意の閉じた経路に対
して
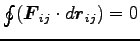 が満され、
が満され、
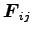 は
ポテンシャル
は
ポテンシャル
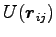 の偏微分 (にマイナス符号をつけたもの) で
表される。つまり
の偏微分 (にマイナス符号をつけたもの) で
表される。つまり
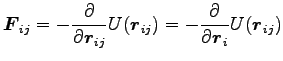 |
|
|
(0) |
ここに、
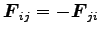 より、
より、
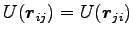 である。
である。
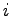 を固定して
を固定して 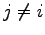 で和をとると
で和をとると
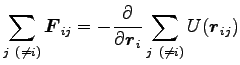 |
|
|
(0) |
そこで
 |
|
|
(0) |
とすると
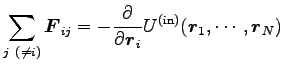 |
|
|
(0) |
であることが示せる。
実際
ここで、2 行目の 2 項目で
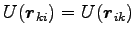 を用い、そのあと
を用い、そのあと
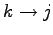 とした。
とした。
更に、もし内力が中心力 1
であるとすると、
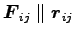 より
より
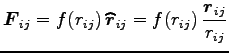 |
|
|
(0) |
と書ける。ここに、
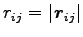 は質点
は質点 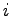 と質点
と質点 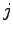 の間の距離、
の間の距離、
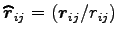 は質点
は質点 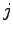 から質点
から質点 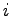 に
至る変位ベクトルの方向 (単位ベクトル) を表す。 そこで
に
至る変位ベクトルの方向 (単位ベクトル) を表す。 そこで
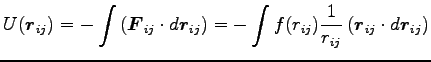 |
|
|
(0) |
ここに、
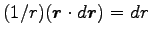 (
(
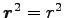 を微分せよ) より
を微分せよ) より
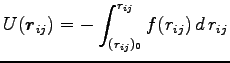 |
|
|
(0) |
エネルギーの原点を
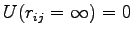 と選ぶと
と選ぶと
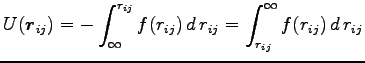 |
|
|
(0) |
この時、
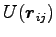 は
は
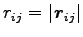 だけの函数である。
特に、万有引力の時は
だけの函数である。
特に、万有引力の時は
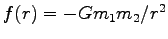 より
より
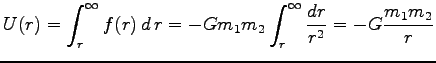 |
|
|
(0) |
これを、万有引力ポテンシャルという。
一般の保存力の場合に戻って、Eq. (6.43) の
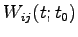 は
は
ここに
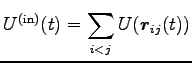 |
|
|
(0) |
を内部位置エネルギーという。これを使うと Eq. (6.44) は
![$\displaystyle [T(t)+U^{(\rm in)}(t)]-[T(t_0)+U^{(\rm in)}(t_0)]
=\sum_i W^{(o)}_i(t; t_0)$](img196.png) |
|
|
(0) |
となる。更に、外力も保存力なら、外力
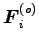 の
ポテンシャルを
の
ポテンシャルを
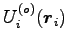 、全系の外力による位置エネルギーを
、全系の外力による位置エネルギーを
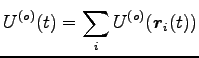 |
|
|
(0) |
として
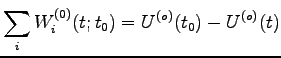 |
|
|
(0) |
より
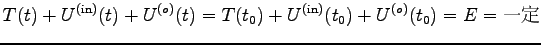 |
|
|
(0) |
これを、質点系の全力学的エネルギーという。
まとめると、「内力も外力も保存力の時、質点系の全力学的エネルギーは
保存する。」
 を質点系の位置エネルギー
(ポテンシャルエネルギー) という。また
を質点系の位置エネルギー
(ポテンシャルエネルギー) という。また
より、質点系の運動方程式は
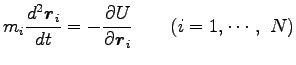 |
|
|
(0) |
とも書ける。
(重心運動の分離) (内力、外力とも保存力とする。)
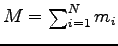 ,
,
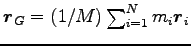 として、
として、
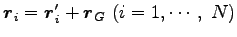 とすると、
とすると、
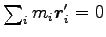 より
より
ここに
質点系の全エネルギーは
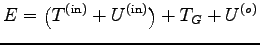 |
|
|
(0) |
ここに
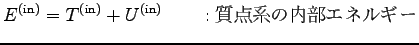 |
|
|
(0) |
は、
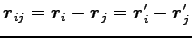 より、
重心に対する相対座標とその速度のみで表されている。
特に、孤立系では
より、
重心に対する相対座標とその速度のみで表されている。
特に、孤立系では 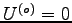 より、重心運動の運動方程式は
より、重心運動の運動方程式は
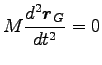 |
|
|
(0) |
そこで、1 質点の場合と同様 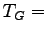 一定。
これと全エネルギーの保存則とあわせて
一定。
これと全エネルギーの保存則とあわせて
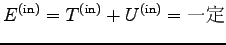 |
|
|
(0) |
すなわち、「孤立系では内部エネルギーが保存する。」
特に、2 質点系では
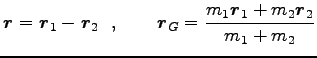 |
|
|
(0) |
により、相対座標と重心座標への変換を行うと、
 は
Eq. (6.17) の相対運動の運動エネルギー
は
Eq. (6.17) の相対運動の運動エネルギー 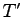 である。
である。



: 中心力による運動
: 物理学基礎論 A
: 角運動量と力のモーメント
Yoshikazu Fujiwara
平成19年7月8日
![]() (
(
![]() ) をもつ質点の集りである。
ここでは、質点系の運動方程式や種々の保存則について調べる。
) をもつ質点の集りである。
ここでは、質点系の運動方程式や種々の保存則について調べる。
![]() 各質点の運動量を
各質点の運動量を
![]() とすると、運動方程式は (慣性系で)
とすると、運動方程式は (慣性系で)
![]()
![]() (ここに、
(ここに、
![]() は質点系の全質量) が座標原点にある座標系
を重心系という。そのような座標系での位置ベクトルは
は質点系の全質量) が座標原点にある座標系
を重心系という。そのような座標系での位置ベクトルは
![]() とする。
まず、外力が働かないから、全運動量は保存される。
とする。
まず、外力が働かないから、全運動量は保存される。
![]() 個の質点系を考え、
個の質点系を考え、
![]() を簡単のため
を簡単のため ![]() と書く。
質点系の全角運動量は
と書く。
質点系の全角運動量は
![]() かつ
かつ
![]() (系の重心)
として、Eq. (6.6) の相対座標を用いると、
(系の重心)
として、Eq. (6.6) の相対座標を用いると、
![]() より
より
![]() との内積をとり、
との内積をとり、![]() で
和をとると
で
和をとると
![]() が相対ベクトル
が相対ベクトル
![]() だけの函数で、かつ
保存力であるとすると、任意の閉じた経路に対
して
だけの函数で、かつ
保存力であるとすると、任意の閉じた経路に対
して
![]() が満され、
が満され、
![]() は
ポテンシャル
は
ポテンシャル
![]() の偏微分 (にマイナス符号をつけたもの) で
表される。つまり
の偏微分 (にマイナス符号をつけたもの) で
表される。つまり
![]() より
より
![]() は
は
![]() ,
,
![]() として、
として、
![]() とすると、
とすると、
![]() より
より