はじめに
中学校と高等学校で学ぶ数学は大きく分けて、1:代数分野、2:幾何分野、3:解析分野という3つの分野に分類される。代数では数式の計算、展開公式、因数分解、方程式や簡単な関数のグラフ等について学ぶ。二項係数の計算に必要な、順列組み合わせ等についても学ぶ。二次方程式の解の公式や判別式、複素数についても必要に応じて学ぶ。ベクトルや簡単な行列と行列式の性質についても学ぶかもしれない。幾何学は円や三角形、四角形等の図形の性質を取り扱う分野で、三角形の合同、相似、平行線の定理、三角形の内角の和等について学ぶ。円と三角形の関係、図形の面積や体積等も取り扱う。ギリシャ時代の数学者ユークリッドによるユークリッド幾何学がその内容である。簡単な三角法もここで学ぶ。戦前の旧制中学の課程では幾何は大変重要な分野であり、アポロニウスの円等結構難しい内容も教えられていたが、新課程ではこれらは、発見的発想なしに直交座標を用いた解析幾何学的手法により全て解けるということで大幅に縮小された。しかし、補助線を1本引いて明快に証明できる問題が多いのは、学んでいて楽しいと思う。解析分野は数列、級数、極限、微分、積分等を学ぶ。三角関数は幾何分野でも出てくるが、解析分野の重要なテーマである。それは複素数を通じて指数関数と密接に結びついている。複素平面の概念はそれらを理解する上で大変有益である。座標系やベクトル、微分積分は物理学を学ぶ上で最小限必要な数学である。また、そこに至るまでの数学は、物理学に限らず全ての学問の基礎であるので、大学に入るまでにしっかり学んでおいてほしいと思う。
数式の変形、展開定理
代数とは読んで字のごとく数字の代わりに文字を使うということである。 例えば辺の長さが \( a, b, c\) の三角形と言う場合、\(a, b, c \) はある条件を満たす任意の数(実数)と考える。また、三角形の面積の公式は、面積= (2分の1)×底辺×高さ、であるが、これを \( S=\frac{1}{2}ah \) と書く。面積は平方(2乗)を表わす英語 Square を用いて大文字の \(S\) で表すのが普通である。\(a\) は底辺の長さ、\(h \) は英語の height から三角形の高さを表す。 数字と文字の混ざったものを数式と言うが、そこでは普通、掛け算の記号 \(×\) は・(中点)と書いたり、誤解が生じない限り全く省略したりするのが普通である。
また別の例は、鶴亀算の時の様に未だわからない数(未知数と言う)を \(x\)とか \(y\)とかで表わすことである。例えば、「鶴と亀が全部で5匹いて足が14本あるとすれば、それぞれ何匹ずつか?」という問題を考える。鶴と亀がそれぞれ \(x\) 匹、\(y\) 匹いるとして、「全部で5匹」ということを \( x+y=5 \) と表し、「足が全部で14本がある」ということを \( 2x+4y=14\)で表す。すなわち
\[ x+y=5 \\ 2x+4y=14 \]
これを、二元一次連立方程式という。あとは、これらを計算の規則に従って解く。まず、\(x+y=5 \)の両辺を2倍して \(2x+2y=10\)。\(2x+4y=14\) から、これを辺々引いて \(2y=4\)。そこで \(y=2\)。これを \(x=5-y\) に代入して \(x=5-2=3\)。結局、\(x=3, y=2\) となって、鶴が3匹、亀が2匹であることが分かる。このプロセスを方程式を解くという。
ここで使っている計算の規則は
1. 等式の両辺に同じ数を掛けたり、(0 以外の)同じ数で割ったりしても変わらない。また、等式の両辺に同じ数を足したり、引いたりしても変わらない
2. 二つの等式がある時、左辺は左辺、右辺は右辺で二つの式を加えたり、引いたりしても構わない。(これを、辺々加えるとか、辺々引くとかいう。)
の二つだけである。これらはいずれも、数については当然成り立つ計算の規則である。それを数式に対しても成り立つと考えるのである。これらは等式に対する計算の規則だが、それ以外に「数について」のところで学んだ四則演算に関する計算の規則がある。もう一度それを書いておくと
(交換則) \( \quad a+b=b+a \quad , \quad ab=ba \)
(結合則) \( \quad (a+b)+c=a+(b+c) \quad , \quad (ab)c=a(bc) \)
(分配則) \( \quad a(b+c)=ab+ac \quad , \quad (a+b)c=ac+bc \)
\( a, b, c \) が如何なる数式であっても、これらが厳密に成り立つと仮定する。更に計算の順序に関する規則や、「数について」のところで学んだ指数法則や対数法則も意味のある限り全ての数式に対して成り立つと考える。
数式に対する計算の規則を駆使して、色々な式を変形していくことが出来る。例えば
\[ (a+b)^2=a^2+2ab+b^2 \] は上の分配則の二番目の式で \(c=a+b\)とおいて、一番目のルールを使うと
\[ (a+b)^2 = (a+b)(a+b)=a(a+b)+b(a+b) \\ = a^2+ab+ba+b^2 = a^2+2ab+b^2 \]
また、\(c=a-b\) と置いて
\[ (a+b)(a-b)=a(a-b)+b(a-b)=a^2-ab+ba-b^2\\ =a^2-b^2 \]
が得られる。これを「和差の積の公式」と言って、「二つの数の和と差の積は、自乗の差」と覚えておくと便利である。これらの式は2つの式の積を解きほぐす公式で展開式と呼ばれる。これらは \(a, b\) が何であっても成り立つ式で、恒等式と言われる。(これに対して鶴亀算の時の \(x, y\) は或る特定の数 \(x=3, y=2\) に対してのみ成り立つので、恒等式ではなく方程式である。) 右辺の \( a^2+2ab+b^2 \) や \(a^2-b^2 \) は、\(a, b\) の多項式、それらを形作る \( a^2 \) や \( b^2, 2ab \) 等を単項式と言う。上の式で \(b\) を \(-b \) に変えると
\[ (a-b)^2=a^2-2ab+b^2 \]
が得られる。(「和差の積」の公式で \(b\) を \(-b\) と変えても、新しい公式は何も得られない。) また、 \(a\) を \(x\)、\(b\) を1 に変えると
\begin{align} (x+1)^2 &=x^2+2x+1 \\ (x-1)^2 &=x^2-2x+1 \\ (x+1)(x-1) &=x^2-1 \end{align}
が得られる。これらはいずれも、上の2つの公式の特別の場合である。
定数 \(a, b, c, ...\)、未知数 \(x, y, ...\) と並んでもう一つの文字の使い方は、あとで関数の所で出てくる変数 (変動する数という意味) である。これにも \(x, y, z, ...\) が使われる。これらを定数とは明確に区別して使うと、十進数の位取りを使った数の組み算と同様に数式の組み算を行うことができる。(図1 参照) 例えば、\(a, b, c, ..\) を 0, 1, 2, ..., 9、\(x=10\) と考えるのである。図1 左図の様な足し算、掛け算と同様に、数式の引き算、割り算も組み算で行なうことが出来る。また、\(x\) の 2 次式で1番一般的な展開公式は
\[ (ax+b)(cx+d)=acx^2+(ad+bc)x+bd \]
である。この公式は、図1 右図のように組み算でも「襷(たすき)がけ」のルールで求められる。「襷がけ」のルールは、分配則を複数回適用したものである。
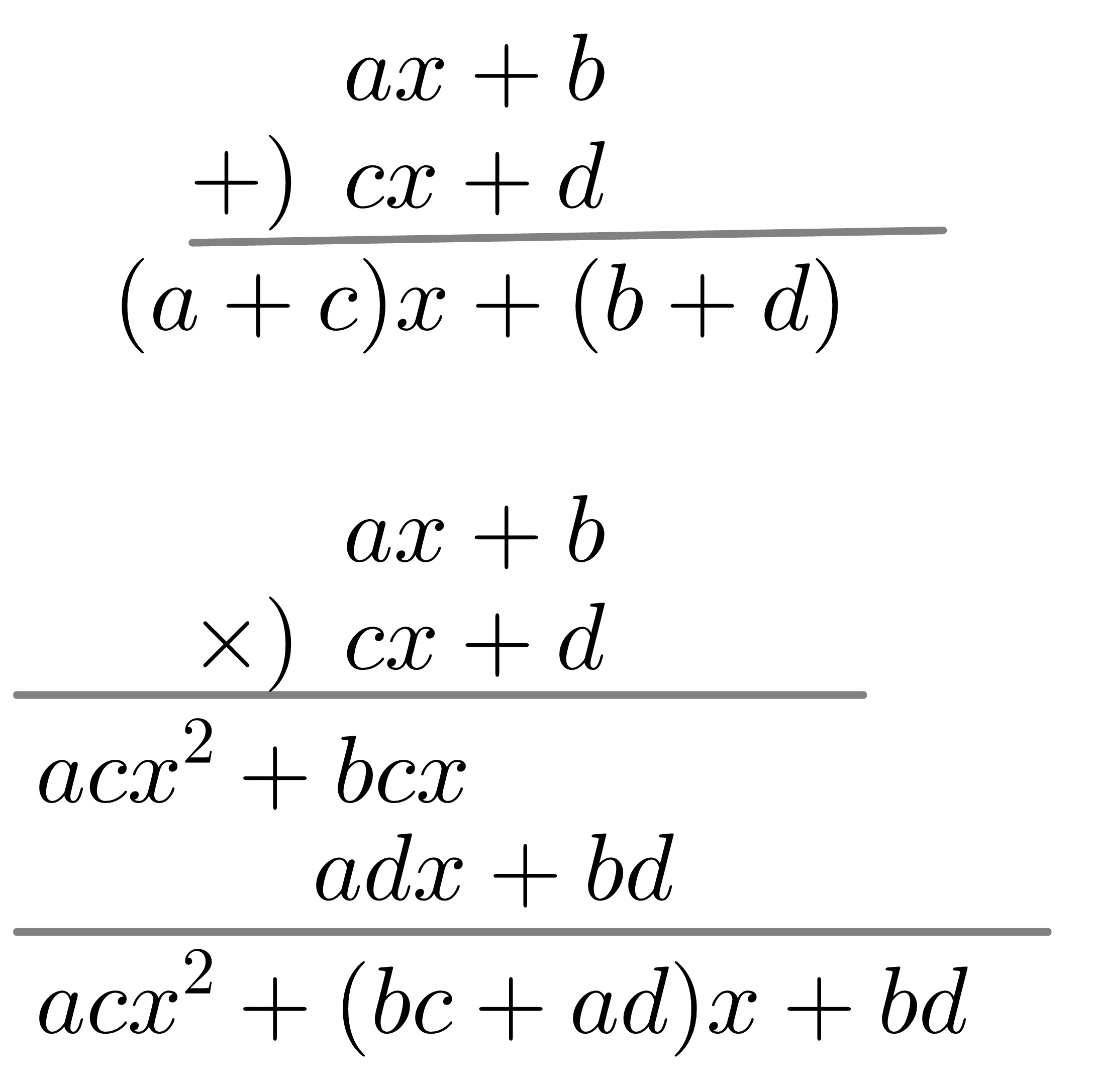
図1-1: 数式の組み算
足し算と掛け算
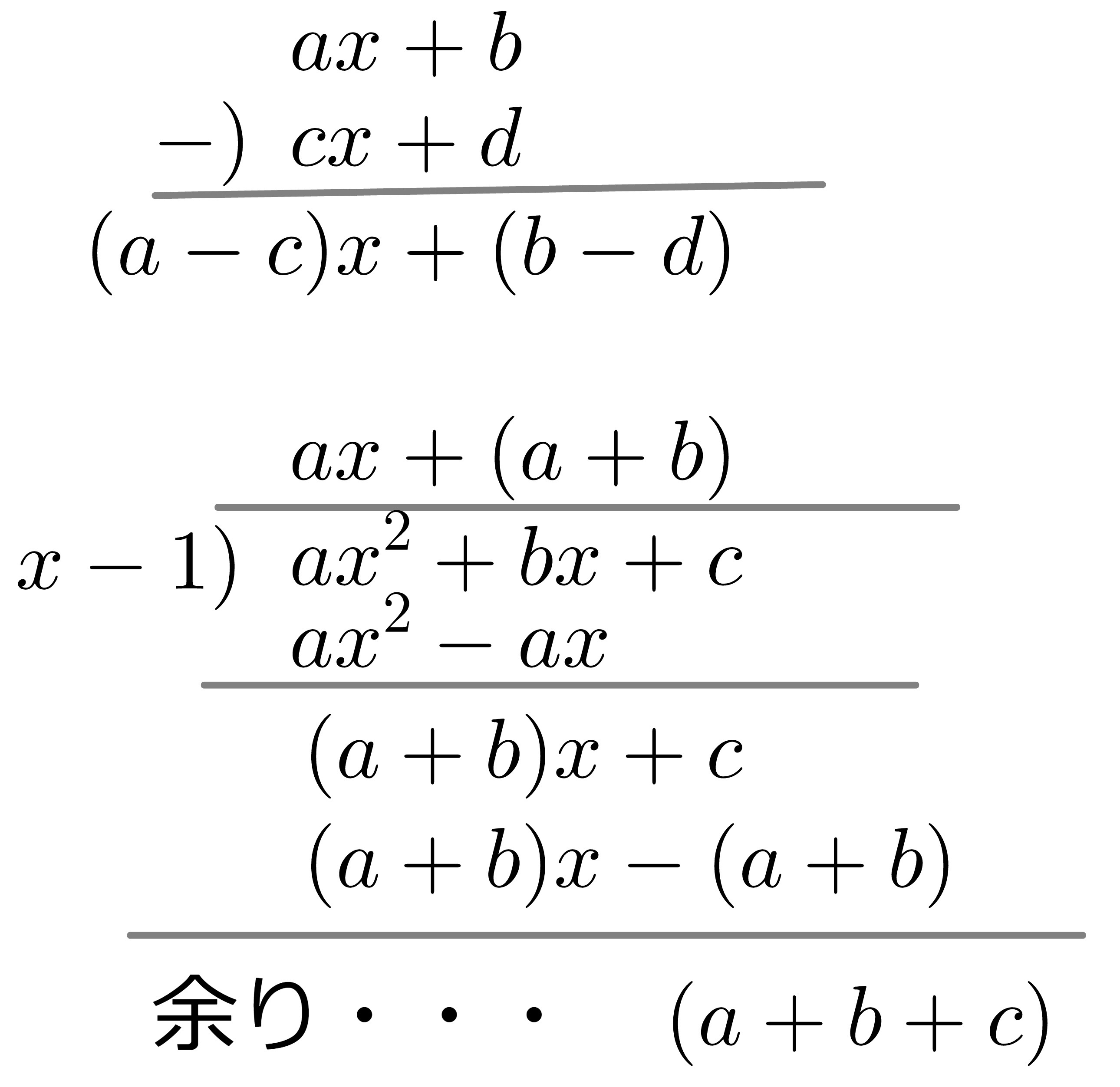
図1-2: 数式の組み算
引算と割り算
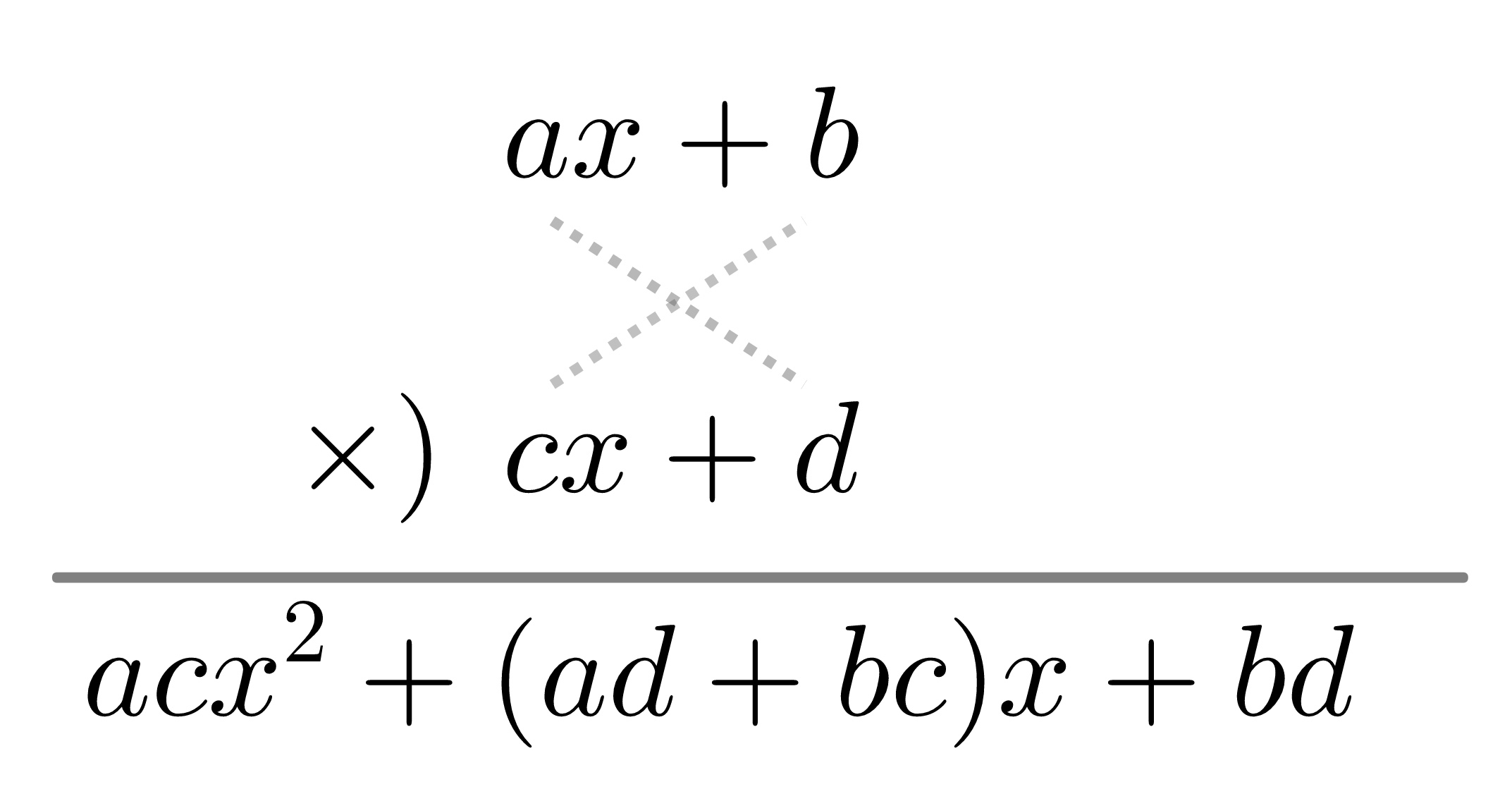
図1-3: 掛け算の襷(たすき)がけのルール
二項定理、パスカルの三角形
\( (a+b)^2 \) の展開公式は、\( (a+b) \) を次々と掛けて行って分配則を何回か使うことにより、更に高次の展開公式に拡張出来る。例えば
\begin{align} (a+b)^3 &=(a+b)^2 (a+b)=(a^2+2ab+b^2)(a+b) \\ &=a^3+2a^2b+ab^2+a^2b+2ab^2+b^3 \\ &=a^3+3a^2b+3ab^2+b^3 \\ (a+b)^4 &=a^4+4a^3b+6a^2b^2+4ab^3+b^4 \\ (a+b)^5 &=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5 \\ ... & ... \end{align}
一般に \(n\) を自然数として、\( (a+b)^n \) の展開公式を二項定理と言い
\[ (a+b)^n = a^n+n a^{(n-1)}b+\frac{n(n-1)}{2} a^{(n-2)}b^2 +... \\ +\frac{n(n-1)(n-2)...(n-r+1)}{r!} a^{(n-r)}b^r +... \\ +\frac{n(n-1)}{2} a^2b^{(n-2)}+n ab^{(n-1)}+b^n \tag{3-1} \]
と表わされる。ここに \( n! \) は「数について」のネピア数の所で出て来た \( n \) の階乗 (factorial) で
\[ n! = 1・2・3・...・n \]
である。これは \(n\) 個の異なる物を並び変える場合の数である。例えば \(1, 2, 3,..., n \) を並べ変える方法は、まず最初に\(n\) 個の中から一つ選び出す方法は \(n \) 通り。次に、そのそれぞれの場合について、残りの \(n-1 \) 個から一つ選び出す方法が \(n-1\) 通り。そこで、ここまでで \(n(n-1)\) 通り。それらのそれぞれに対して、残りの \(n-2\) 個から一つ選び出す方法が \(n-2\) 通りだから、全部で \(n(n-1)(n-2)\) 通り。このプロセスをくりかえして、最後に 1 個一通りが残る。従って \( n(n-1)(n-2)...2・1=n! \) 通りとなる。(分かりにくければ、1, 2, 3 の並び変え、\(3!=3・2・1=6\) で確かめてみよ。) また、0 の階乗は \( 0!=1 \) と考える。 \( (a+b)^n \) の展開の式で右辺各項 は全て
\[ 係数×a^{(n-r)}b^r \quad \hbox{with} \quad \ r=0, 1, ..., (n-1), n \]
のかたちをしている。\( r\) が上の何であっても、\(a \) のベキ乗と \(b \) のベキ乗を足し合わせると恒に \( (n-r)+r=n\) となるので、これらを \(a \) と \(b \) の \(n \)次同次式という。また、係数は分母、分子に \( (n-r)! \) を掛けると
\[ \frac{n(n-1)(n-2)...(n-r+1)}{r!} \\ =\frac{n(n-1)(n-2)...(n-r+1)(n-r)(n-r-1)...・2・1}{r! (n-r)!} \\ =\frac{n!}{r! (n-r)!} \]
となるので、これを \( \binom{n}{r} \) とか \( \hbox{}_nC_r \) とか書いて二項係数 (binomial coefficient) という。二項係数は、後でみるように \(n \) 個の物から順番を考えずに \(r \) 個取り出す取り出し方の数である。特に \( \binom{n}{0}=\binom{n}{n}=1, \binom{n}{1}=\binom{n}{n-1}=n, \binom{n}{2}=\binom{n}{n-2}=\frac{n(n-1)}{2}, ... \)である。 展開式で \( \binom{n}{r} a^{(n-r)} b^r \) の単項式を一般項という。二項定理は一般項を \(r=0 \) から \(n \) まで加え合わせて
\[ (a+b)^n=\Sigma_{r=0}^\infty \binom{n}{r} a^{(n-r)} b^r \]
と表わされる。ここに \( \Sigma \) は英語の「和」Sum の S に対応する大文字のギリシャ語のアルファベットで、その右にある一般項を \(r=0 \) から \(n \) まで加え合わせることを意味する。
二項係数の意味は
\[ (a+b)^n=(a+b)(a+b)...(a+b) \]
で \(n \) 個並んだ \( (a+b) \) から \(b \) を \(r \) 個選び出す出し方を数える事から明らかになる。今右辺で、\( (a+b) \) を左から順番に \( 1, 2, ..., n \) と番号を付けて \(b \)を \(r \) 個選び出す方法は \( n(n-1)...(n-r+1) \) 通りあるが、これらの \(r \) 個の番号は実は全て同じ \(b \) だから \(r \) 個の数字の並び変えの数 \(r! \) だけ重複している。そこで、これを \( r! \) で割って
\[ \binom{n}{r}=\frac{n(n-1)(n-2)...(n-r+1)}{r!}=\frac{n!}{(n-r)! r!} \]
が求める数である。二項係数はまた、次の関係式を満たす。
\[ \binom{n}{r}+\binom{n}{r+1}=\binom{n+1}{r+1} \]
実際
\[ 左辺 =\frac{n!}{(n-r)! r!}+\frac{n!}{(n-r-1)!\ (r+1)!} \\ =\frac{n!}{(n-r)! (r+1)!}・(r+1)+\frac{n!}{(n-r)! (r+1)!}・(n-r) \\ =\frac{(n+1)!}{(n-r)! (r+1)!} = \binom{n+1}{r+1}=右辺 \]
上の式は、\(n \) 次式の係数と \( \binom{n+1}{0}=\binom{n+1}{n+1}=1 \) を用いて、\( n+1 \) 次の展開式の二項係数を次々に求めていけるので漸化式と言われる。これを図式化したものがパスカルの三角形である。パスカルの三角形を作るには、まず \( (a+b) \) の \(a \) と \(b \) の係数 1 1 を一番上の段に書く。次にこれらを加えた 2 をすぐ下の段に書く。次にその両端に1 ... 1 を補って 1 2 1 とする。これは \( (a+b)^2 \) の展開公式の係数である。次に隣り合う 1 2, 2 1 をそれぞれ加えて 3 3 をすぐ下の段に書く。再び左右に 1 を補って 1 3 3 1 とすれば、これは \( (a+b)^3 \) の展開係数である。この操作を繰り返して \( (a+b)^4 \) の展開係数 1 4 6 4 1、\( (a+b)^5 \) の展開係数 1 5 10 10 5 1 が次々と得られる。

図2: パスカルの三角形
\( (a+b)^n \) の展開公式で \(a \) を \(x \)、\(b \) を 1 と置くと
\[(x+1)^n=x^n+\binom{n}{1} x^{(n-1)}+... \\ +\binom{n}{r} x^{(n-r)}+...+\binom{n}{n} x+1 =\Sigma_{r=0}^n \binom{n}{r} x^{(n-r)} \tag{3-2} \]
が得られる。このように \(x \) の \(n \) 次式を \(x \) のベキ指数が小さくなっていく順に項を並べることを \(x \) の降ベキの順に式を整理するという。また逆に、\( 1, x, x^2, ..., x^n \) の順に並べる事を昇ベキの順に式を整理するという。(3-1) の展開式は、\(a \) については降ベキの順に、\(b \) については昇ベキの順に並べられている。(3-2) は(3-1) の特別の場合なので、一般には (3-2) から (3-1) を再現することは出来ない。しかし、\( (a+b)^n \) の場合には、これが a と b の同次式である事を用いて (3-2) から (3-1) を再現出来る。\( (a+b)^n \) が \(a \) と \(b \) の同次式である事は \(a \) を \( ka \), \(b \) を \(kb \) と変えて
\[ (ka+kb)^n=(k(a+b))^n=k^n (a+b)^n \]
の様に元の式に \( k^n \) が掛かる事から確かめられる。同様に \(a \) と \(b \) からなる単項式で \(n \) 次の同次式となるのは \( a^{(n-r)}b^r \) の形の単項式だけである。従って、\( (a+b)^n \) は必ず \( a^{(n-r)}b^r\) \( (r=0, ..., n) \) の重ね合わせで書けるはずであり、その様な式で \(a \) を \(x \), \(b \) を 1 と置き換えて (3-2) になるのは、(3-1) の形しかあり得ない。
二項定理 (3-2) で \(x=1 \)と置くと二項係数の和の公式
\[ \Sigma_{r=0}^n \binom{n}{r} = 2^n \]
が得られる。また、(3-2) で \(x \) を \( -x\) に変えて、全体の符号を変えると
\[ (x-1)^n=\Sigma_{r=0}^n (-)^r \binom{n}{r} x^{(n-r)} \tag{3-3} \]
が得られる。ここに \( (-)^r \) は \( (-1)^r \) の意味である。ここで、更に \(x=1 \) と置くと
\[ \Sigma_{r=0}^n (-)^r \binom{n}{r} = 0 \quad \hbox{for} \quad n = 1, 2, 3, ... \]
が得られる。実際
\begin{align} 1+1 &=2 \\ 1+2+1 &=2^2 \\ 1+3+3+1 &=2^3 \\ 1+4+6+4+1 &=2^4 \\ 1+5+10+10+5+1 &=2^5 \\ ... &... \\ 1-1 &=0 \\ 1-2+1 &=0 \\ 1-3+3-1 &=0 \\ 1-4+6-4+1 &=0 \\ \end{align}
が成り立っている。
(追補-1) : 多項定理への拡張
二項定理で \( n-r=n_1, r=n_2 \)として \(n_1+n_2=n \) と書き
\[ (a+b)^n=\Sigma_{n_1+n_2=n} \left( \frac{n!}{n_1! n_2!}\right) a^{n_1} b^{n_2} \]
とすると、三項定理や更に一般的な N-項定理への拡張が容易である。ここに \( \Sigma_{n_1+n_2=n} \) は、\( n_1, n_2 \) を (0 を含む) 負でない整数として \( n_1+n_2=n \) を満たす全ての pair \( (n_1, n_2)=(n, 0), (n-1, 1), (n-2, 2), ... , (1, n-1), (0, n) \) について和を取ることを示す。例えば、三項定理は
\[ (a+b+c)^n =\Sigma_{n_1+n_2+n_3=n} \left( \frac{n!}{n_1! n_2! n_3!}\right) a^{n_1} b^{n_2} c^{n_3} \]
と表わされる。・・・ 一般にN-項定理は
\[ (a_1+a_2+a_3+...+a_N)^n \\ =\Sigma_{n_1+n_2+n_3+...+a_N=n} \left( \frac{n!}{n_1! n_2! n_3! ... n_N!}\right) {a_1}^{n_1} {a_2}^{n_2} {a_3}^{n_3} ... {a_N}^{n_N} \]
である。ここに \( (n_1, n_2, n_3, ... , n_N) \) は
\[ n_1+n_2+n_3+...+n_N=n \quad \hbox{with} \quad n_1, n_2, n_3, ... , n_N \in \{0\} \cup \boldsymbol{N} \]
を満たす全ての解について取るものとする。その様な解の個数は
\[ \hbox{}_{n+N-1}C_n=\frac{(n+N-1)!}{n! (N-1)!} \]
である。この数は、\( n \) 個の同種粒子を \( n_1, n_2, n_3, ... , n_N \) と番号の付いた \( N \) 個の箱に詰める詰め方の数であって、次の様に考える事によって得られる。まず、\( n_N \) 番の箱は一番右に置くこととして、\( N-1 \) 個の箱と \( n \) 個の粒子を一緒にして全部で \( n+N-1 \) 個の物の並び替えを考える。区切られた粒子は全てすぐ右の箱に入れると考える。粒子は全て同じだから、\( (n+N-1)! \) を \( n! \) と \( N-1 \) 個の箱の並び替え \( (N-1)! \) で割ると上の数が得られる。
例えば、\( N=3 \) の時、\( (n_1, n_2, n_3) \) の組みの数は \( \hbox{}_{n+2}C_n=\hbox{}_{n+2}C_2=(1/2)(n+2)(n+1) \) である。そこで、もし\( n=3 \) なら \( (n_1, n_2, n_3)=(3, 0, 0), (0, 3, 0), (0, 0, 3), (2, 1, 0), (2, 0, 1), (1, 2, 0), \) \( (0, 2, 1), (1, 0, 2), (0, 1, 2), (1, 1, 1) \) の10個の組み合わせが可能で
\[ (a+b+c)^3=a^3+b^3+c^3+3(a^2 b+a^2 c+a b^2+b^2 c+a c^2+b c^2) \\ +6abc \]
となる。二項係数の和の公式は、今の場合
\[ \Sigma_{n_1+n_2+n_3=n} \left( \frac{n!}{n_1! n_2! n_3!} \right)=3^n \\ ... \\ \Sigma_{n_1+n_2+n_3+ ... +n_N=n} \left( \frac{n!}{n_1! n_2! n_3! ... n_N!} \right) =N^n \]
となる。
「和差の積の公式」の一般化
\( (x-1)(x+1)=x^2-1 \) を一般化して次の展開公式が得られる。
\[ (x-1)(x^2+x+1)=x^3-1 \\ (x-1)(x^3+x^2+x+1)=x^4-1 \\ .... \]
一般に任意の自然数 \( n\) に対して
\begin{align} (x-1)(x^n+x^{(n-1)}+...+x+1)=x^{(n+1)}-1 \tag{4-1} \end{align}
これらは、分配法則を繰り返し使うことにより簡単に証明出来る。 ここで、更に \( x \) を \( -x \) と変えると
\begin{align} & (x+1)(x-1)=x^2-1 \\ & (x+1)(x^2-x+1)=x^3+1 \\ & (x+1)(x^3-x^2+x-1)=x^4-1 \\ & ... \\ & (x+1)(x^n-x^{(n-1)}+....+(-1)^{(n-1)} x+(-1)^n) \\ & =x^{(n+1)}+(-1)^n \tag{4-2} \end{align}
が得られる。また、二項定理のところで見た様に同次式の性質を用いると、(4-1) と (4-2) の公式を次の様に一般化出来る。
\begin{align} & (a-b)(a^n+a^{(n-1)} b+...+ab^{(n-1)}+b^n) \\ & =a^{(n+1)}-b^{(n+1)} \\ & (a+b)(a^n-a^{(n-1)} b+...+(-1)^{(n-1)}ab^{(n-1)}+(-1)^n b^n) \\ & =a^{(n+1)}+(-1)^n b^{(n+1)} \tag{4-3} \end{align}
更に、(4-1) を \( x \neq 1\) として
\begin{align} 1+x+x^2+...+x^n=(x^{(n+1)}-1)/(x-1) \\ =(1-x^{(n+1)})/(1-x) \quad (n \neq 1) \tag{4-4} \end{align}
例えば \( x=2 \)と置くと
\[ 1+2+2^2+2^3+...+2^n=2^{(n+1)}-1 \]
また、\( x=\frac{1}{2} \)と置くと
\[ 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^n}=2-\frac{1}{2^n} \]
が得られる。更に、\( n→ \infty \)と置くと、\( \frac{1}{2^n} → 0 \) だから
\[ 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+.. .= 2 \tag{4-5} \]
もう一つの例として \( x=-1/2 \)と置くと
\[ 1-\frac{1}{2}+\frac{1}{2^2}-\frac{1}{2^3}+\frac{1}{2^4}-.. .= \frac{2}{3} \tag{4-6} \]
(練習問題-1)(4-1)と (4-2) を用いて (4-3) を示せ。
(練習問題-2) 電卓を使って、(4-5), (4-6) が成り立っている事を確かめよ。
(注意) ここで述べた公式は、あとで「解析分野」で学ぶ「等比級数」の公式である。
(もう一つの展開公式) 前節で学んだ「二項定理」と「等比級数」の展開公式以外に、知っておくと便利な公式として
\[ (a+b+c)(a^2+b^2+c^2-ab-bc-ca) \\ =a^3+b^3+c^3-3abc \tag{4-7} \]
がある。(分配則を何回か使って証明せよ。)更に、ここで
\[ a^2+b^2+c^2-ab-bc-ca \\ =\frac{1}{2}[(a-b)^2+(b-c)^2+(c-a)^2] \tag{4-8} \]
を使うと、\( a, b, c \) が実数の時
\[ a+b+c ≧ 0 ←→ a^3+b^3+c^3-3abc ≧ 0 \]
が成り立つ。更に、特に \( a^3+b^3+c^3-3abc=0 \) の時、\( a+b+c=0 \) か \( a=b=c \) かどちらかが成り立つ。 この公式は、複素数まで考えた時、あとで3次方程式の根の公式 (カルダノの式) を導くためにも用いられる。
因数分解、方程式の解、複素数の必要性
展開公式を右辺、左辺逆向きに見なしたものが、因数分解の公式である。これは「数について」で学んだ数についての素因数分解を数式にまで拡張したものである。因数分解は方程式を解くために絶対に必要である。例えば
\[ x^2-3x+2=0 \]
を解くためには、左辺を \( (x-1)(x-2) \) という風に因数分解しておけば
\[ (x-1)(x-2)=0 \]
より、\( x-1=0 \) か \( x-2=0 \) かのどちらかで、ここから \(x=1 \) or \( x=2 \) が求まる。実際、これらが、元の方程式を満たすことは、これらを \( x^2-3x+2 \) に代入して
\[ 1^2-3×1+2=2-3+1=0 \\ 2^2-3×2+2=4-6+2=0 \]
として確かめることが出来る。
覚えておくと便利な公式は
\begin{align} & x^2+(a+b)x+ab=(x+a)(x+b) \\ & x^2-(a+b)x+ab=(x-a)(x-b) \\ & x^2-a^2=(x+a)(x-a) \\ & acx^2+(ad+bc)x+bd=(ax+b)(cx+d) \\ & x^3-1=(x-1)(x^2+x+1) \\ & x^3+1=(x+1)(x^2-x+1) \\ & a^3-b^3=(a-b)(a^2+ab+b^2) \\ & a^3+b^3=(a+b)(a^2-ab+b^2) \\ & a^3+b^3+c^3-3abc \\ & =(a+b+c)(a^2+b^2+c^2-ab-bc-ca) \tag{5-1} \end{align}
等である。積の形に書いた右辺の (...) 内の式のそれぞれを因数とか因子 (factor) とかいう。多くの場合、これらを繰り返し使う事で極限まで因数分解出来る。 例えば、「和差の積」の公式を何回か使うことで
\[ x^4-1=(x^2-1)(x^2+1)=(x+1)(x-1)(x^2+1) \]
が得られる。実数までの範囲内ではここまでである。しかし、「数について」で学んだ複素数を用いれば、\(x^2+1 \) は更に因数分解出来る。虚数単位 \(i \)を用いると \(i^2=-1 \) だから、「和差の積」の公式が複素数までの範囲内でも成り立つとして
\[ x^2+1=x^2-(-1)=x^2-i^2=(x-i)(x+i) \]
と因数分解出来る。そこで \(x \) の4次式 \(x^4-1 \)は
\[ x^4-1=(x+1)(x-1)(x-i)(x+i) \]
と四つの1次式の積に因数分解出来る。従って、4次方程式
\[ x^4-1=0 \]
は複素数の範囲内で \(x=1, -1, i, -i \) の四つの解をを持つ。(一般には、\(x \) は実数解を連想させるので複素数 \(z \) を使って \(z^4-1=0 \)と書く方が良いかもしれないかもしれない。) この様に、これまで扱って来た展開公式や因数分解の公式は、数の概念を実数だけでなく複素数にまで拡張しても成り立つ。実は数式の規則や計算の規則を普通に成り立つ様に仮定すると、必然的に複素数の概念にまで辿り着くのである。
(練習問題-3) \(x^6-1 \) を実数の範囲内で因数分解せよ。複素数の範囲まで広げると \(z^6-1 \) はどこまで因数分解出来るか?(次の項の例題と補遺を参照のこと。)
2次方程式の根の公式、判別式、根と係数の関係
\( x\) の一次式 \(=0 \)と置いた方程式を 1 次方程式という。一番一般的な 1 次方程式は、\(a \neq 0, b \) をある定まった定数として
\[ ax+b=0 \quad (a \neq 0) \]
と表わされる。定数 \(a \)を未知数 \(x \)の係数、\(b \) を定数項という。この方程式の解は
\[ x=-b/a \]
これを 「1 次方程式の解の公式」という。この公式は、\(a, b, x \) が複素数でも成り立つ。すなわち、\( \alpha z + \beta = 0 \) の時 \(z = - \beta / \alpha \) が成り立つ。(勿論 \( \alpha \neq 0 \) )
同様に、\(x \) の 2 次方程式に対しても、一般的な解の公式を求める事が出来る。2次方程式以上の時は解を根ということが多いので、これを2 次方程式の根の公式」という。2 次方程式の一般形は、\(a, b, c \)を \( a \neq 0 \) のある定まった実数 (有理数、整数であることが多い) として
\[ ax^2+bx+c=0 \quad (a \neq 0) \]
と表わされる。まずはじめに、\(a \)は 0 でないから全体を \(a \)で割っておく。
\[ x^2+\frac{b}{a}x+\frac{c}{a}=0 \]
ここで、左辺を次の様に「完全平方」の形に変形する。
\begin{align} & x^2+\frac{b}{a}x+\frac{c}{a}=\left[x^2+2\left(\frac{b}{2a}\right)x+\left( \frac{b}{2a}\right)^2\right]-\left( \frac{b}{2a}\right)^2+\frac{c}{a} \\ & =\left(x+\frac{b}{2a}\right)^2-\left[ \left( \frac{b}{2a} \right)^2 -\frac{c}{a} \right] \\ & =\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{(2a)^2} \tag{6-1} \end{align}
これを 0 と置いて、2 項目を右辺に移行すると
\[ \left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{(2a)^2} \]
が得られる。2 乗して右辺になる量は根号 \( \sqrt{\qquad} \) を使って \( \pm \frac{\sqrt{b^2-4ac}}{2a} \) より ( \( \pm \) を忘れないこと!)
\[ x+\frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a} , \\ x=-\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a} =\frac{-b \pm \sqrt{b^2-4ac}}{2a} \]
結局 \( ax^2+bx+c=0 \quad (a \neq 0) \) の根の公式として
\[ x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \tag{6-2} \]
が得られる。
上の公式で \( D=b^2-4ac \) を二次方程式の判別式という。\( D > 0 \) の時は二次方程式は二つの実数解を持つ。\( D = 0 \) の時は、これらの二つの実数はルートの中が 0 なので一致し、この場合を重根を持つという。一方、\( D < 0 \) の時はルートの中は負の実数になり
\[ \pm \sqrt{D} = \pm \sqrt{|D|} i \]
は純虚数となる。ここに \( |D| \) は負の数 \(D \) の絶対値であり \( |D|=-D>0 \)である。この時、二次方程式の根は二つの互いに共役な複素数
\[ x=\frac{-b \pm \sqrt{|D|} i}{2a} \]
となる。複素数の解の存在は二次方程式の左辺の二次関数を、実数 \( x \) の実数関数 \( f(x)=ax^2+bx+c \) と考えて、\( f(x) \) の表わすグラフを考えてみるとすぐ分かる。\( f(x)=0 \) の時、すなわ放物線と \( x \)-軸の交わる点が二次方程式の根の位置である。\( D < 0 \)の時は、上向き( \(a >0\) ) 下向き( \(a <0\) ) の放物線に関わらず、\(x \)-軸とは交わらない。従って、実数の解はない。\( D=0 \) の時は放物線は頂点を \(x\)-軸に接し、それが重根の位置である。 \( D>0 \) の時は \(x \)-軸と 2 点で交わり、2 つの実数根を持つ。
(6-2) の特別の場合として \(b \) を \(2b \) に変えた
\[ ax^2+2bx+c=0 \quad (a \neq 0) \\ x=\frac{-b \pm \sqrt{b^2-ac}}{a} \tag{6-3} \]
や、\( a=1 \)と置いた
\[ x^2+2bx+c=0 \\ x=-b \pm \sqrt{b^2-c} \tag{6-4} \]
も覚えておくと便利である。
実数根であれ複素数根であれ、これらは元の二次方程式を満たすから、これらの二つの根をギリシャ文字の \( \alpha, \beta \)で表わすと
\[ a \alpha^2 + b \alpha + c = 0 \\ a \beta^2 +b \beta +c = 0 \]
が満たされる。更に、因数分解の公式から
\[ ax^2+bx+c = a (x - \alpha)(x - \beta) \]
が成り立っているはずである。そこで、右辺を展開して左辺の \(b, c \)と比べると
\[ \alpha+\beta = -\frac{b}{a} \ , \quad \alpha \beta = \frac{c}{a} \]
が得られる。これを二次方程式の根と係数の関係という。\(a, b, c \) が実数の時、複素数解に対しては、一番目の式は複素数解 \( \alpha \) と \( \beta \)が互いに複素共役、二番目の式はこれらの複素数の絶対値の 2 乗が実数 ( ≧ 0)であることを示している。実数解の時は \( \pm \sqrt{\qquad} \) 部分が互いに消えて、実数=実数の式になる。
( 追補-1) 二次方程式の根の公式の一つの例として
\[ x^3=1 \]
の3次方程式を考える。右辺の 1 を左辺に移行すると
\[ x^3-1=0 \]
左辺を因数分解すると
\[ (x-1)(x^2+x+1)=0 \]
実数の範囲内では解は \(x=1 \) だけである。実際 \( x^2+x+1 \) の部分は
\[ x^2+x+1=(x+1/2)^2+3/4 > 0 \quad \hbox{for}\ \forall x \in \boldsymbol{R} \]
より決して 0 にはならない。しかし、解の範囲を複素数まで広げると \( x^2+x+1=0 \) に二次方程式の根の公式を使って
\[ x=\frac{-1 \pm i \sqrt{3}}{2} \]
という 2 つの複素共役な複素数解が得られる。このうちの \(+ \) 符号の方の複素数を
\[ \omega=\frac{-1+i \sqrt{3}}{2} \]
と置くと、\(- \) 符号の方の共役複素数は
\[ \omega*=\omega^2=\frac{-1-i \sqrt{3}}{2} \]
と表わされる。実際
\[ \omega^2=\frac{1-3-2i \sqrt{3}}{4}=\frac{-1-i \sqrt{3}}{2} \]
そこで
\[ \omega+\omega^2=-1 \]
これは、\( \omega \)が \( x^2+x+1=0 \) の解であることより当然である。更に
\[ \omega^3=\omega \ \omega^2=\frac{1+3}{4}=1 \]
すなわち、\( \omega \) (と \( \omega^2\) )は \( x^3-1=0 \) の解である。
また、\( \omega \) と \( \omega^2 \) が \( x^2+x+1=0 \) の解である事により、\( x^2+x+1 \) は
\[ x^2+x+1=(x-\omega)(x-\omega^2) \]
と因数分解出来る。実際、右辺を展開すると
\[ 右辺=x^2-(\omega+\omega^2)x+\omega^3=x^2-(-1)x+1=x^2+x+1=左辺 \]
そこで結局 \( x^3-1 \)は
\[ x^3-1=(x-1)(x-\omega)(x-\omega^2) \]
と因数分解出来る。ここで、\(x \) を \(-x \) に変えると
\[ x^3+1=(x+1)(x+\omega)(x+\omega^2) \]
である事も分かる。ここに \( \omega=\frac{-1+i \sqrt{3}}{2} \)である。
(追補-2) ここで述べた 3 次の因数分解の公式は、展開公式
\[ (x+a)(x+b)(x+c)=x^3+(a+b+c)x^2+(ab+bc+ca)x+abc \]
の特別の場合である。つまり、\( a, b, c \) として \(1, \omega, \omega^2 \)や \( -1, -\omega, -\omega^2 \)を選ぶことによって得られる。(確かめてみよ。)
(追補-3) \(n \) を任意の自然数として、\(z^n=1 \) すなわち \(n \) 次方程式 \( z^n-1=0 \) は複素数の範囲内で \(n \) 個の解を持ち、それらは後述する複素平面内の単位円の上に等間隔に分布している。( \(z=1 \) は常に解である。) これを「1 の分解」という。
関数とグラフ、直交座標、方程式との関係
恒等式における定数 \( a, b, c\)、方程式における未知数 \(x, y, z \) と並んで代数の重要なもう一つの応用例として、関数 (函数とも書く) と変数 \(x, y, z \) がある。ここでは特に断らない限り、\(x, y \) は実数、\(z \) は複素数と仮定する。関数とは簡単には「伴って変わる量」とよく言われる。その意味は、例えば \( y=ax+b \) の時、変数 \(x \) が \(x=0, 1, 2, ... \) と変わると \(y \) が \( y=b, a+b, 2a+b, ... \)と変わる事である。その意味で \(y\) もまた変数である。これを \(y\) は \(x \) の関数である (英語では、\(y\) is a function of \(x\) ) と言って、\( y=f(x) \) と書き表わす。\( f(x) \) は具体的な \(x\) への依存性を表わす。今の場合 \( f(x)=ax+b \) である。\(x\) には同じ値が入る。すなわち、\( f(0)=a×0+b=b, f(1)=a×1+b=a+b, \) \(f(2)=a×2+b=2a+b, ... \) 等である。
関数を視覚的に (幾何学的に) わかりやすく表わす方法として、関数のグラフを描く方法がある。そのために、水平方向と垂直方向に二本の数直線を引き、それらをそれぞれ \(x\)-軸、\(y\)-軸と呼び、平面内の点 P (point) を \( (x, y) \) と二つの実数の対 (pair) で表わす。すなわち、P(\(x, y\)) である。これを直交座標とかデカルト座標とか言う。(\(x\)-\(y\) 座標とかユークリッド座標とか言う場合もある。) \(x\)-軸と\(y\)-軸は矢印をつけて正の方向を明示する。また \(x\)-軸と \(y\)-軸の交わった所 P(0, 0) を座標の原点と言い、O (Origin) で表わす。平面上の点は二つの実変数で表わされるので、これを二次元直交座標と言う。我々の住んでいる空間は実は縦、横、高さの三次元なので、もう一つ \(x\)-軸と \(y\)-軸に垂直な方向に \(z\)-軸 (この場合の \(z\) は実数である) を取って、これを三次元直交座標と言う。
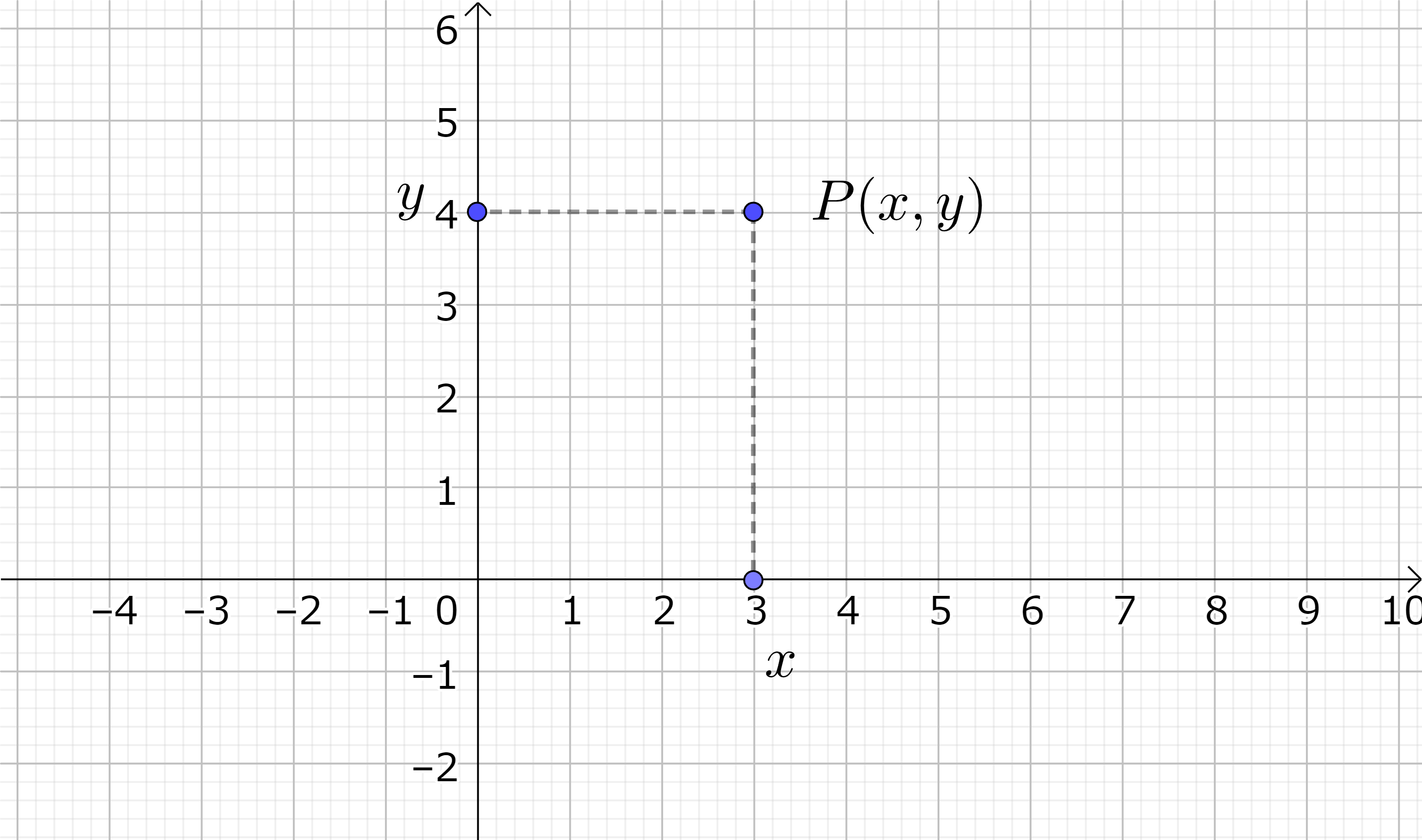
図3-1: 二次元直交(デカルト)座標
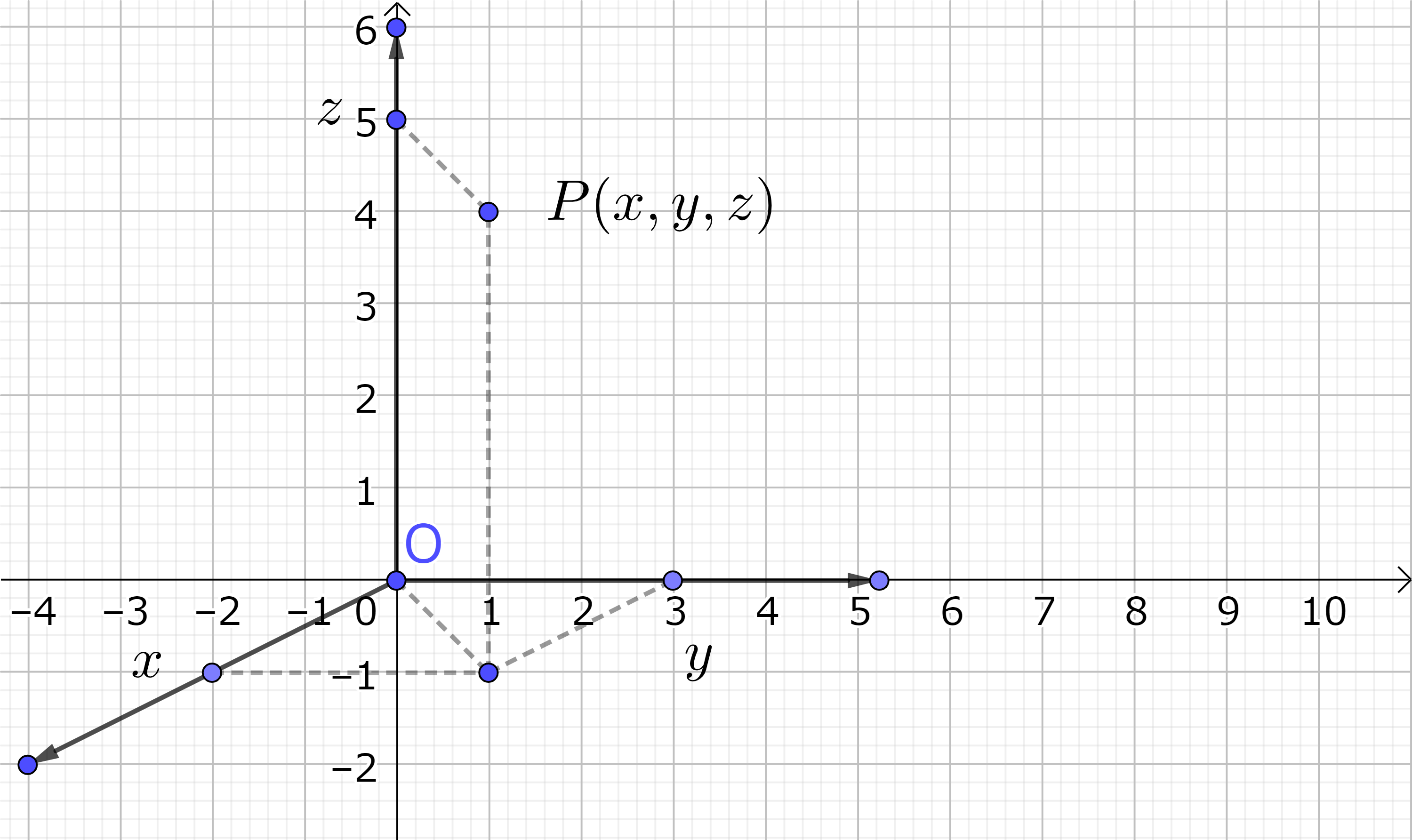
図3-2: 三次元直交(デカルト)座標
\(x\) の一次関数 \(y=ax+b \) のグラフは二次元直交座標の中で、種々の \( x\) に対する点 P(\(x, y\)) を繋いで出来る直線である。\(y\)-軸と交わる点は、\(x=0 \) と置いて得られる P(0, \(b\)) で表わされる点である。これを \(y\)-軸の切片という。\(x\)-軸の切片、即ち \(x\)-軸と交わる点は、\(y=0 \) と置いた方程式 \(ax+b=0 \) を \(x\) について解いて得られる。\(a \neq 0 \) の時は、\(x=-\frac{b}{a} \) という解を求める事が出来て、点 P(\( -\frac{b}{a}, 0\) ) が \(x\)-軸の切片となる。\(a \) を一次関数の傾きと言い、\(x \) が 1 だけ増えた時 \(y \) が幾ら増えるかという量を表わす。\(a=0 \) で \(y=b \) の時 \(b \neq 0 \) なら、\(y=b \) の直線は \(x\)-軸に平行になる。もし更に \(b=0 \) なら、\(y=0 \) は \(x\)-軸を表わす。\(y=ax+b \)で \(b=0\) と置いた \(y=ax \) は \(x\)-軸を \(a \) だけ傾けた原点を通る直線になる。
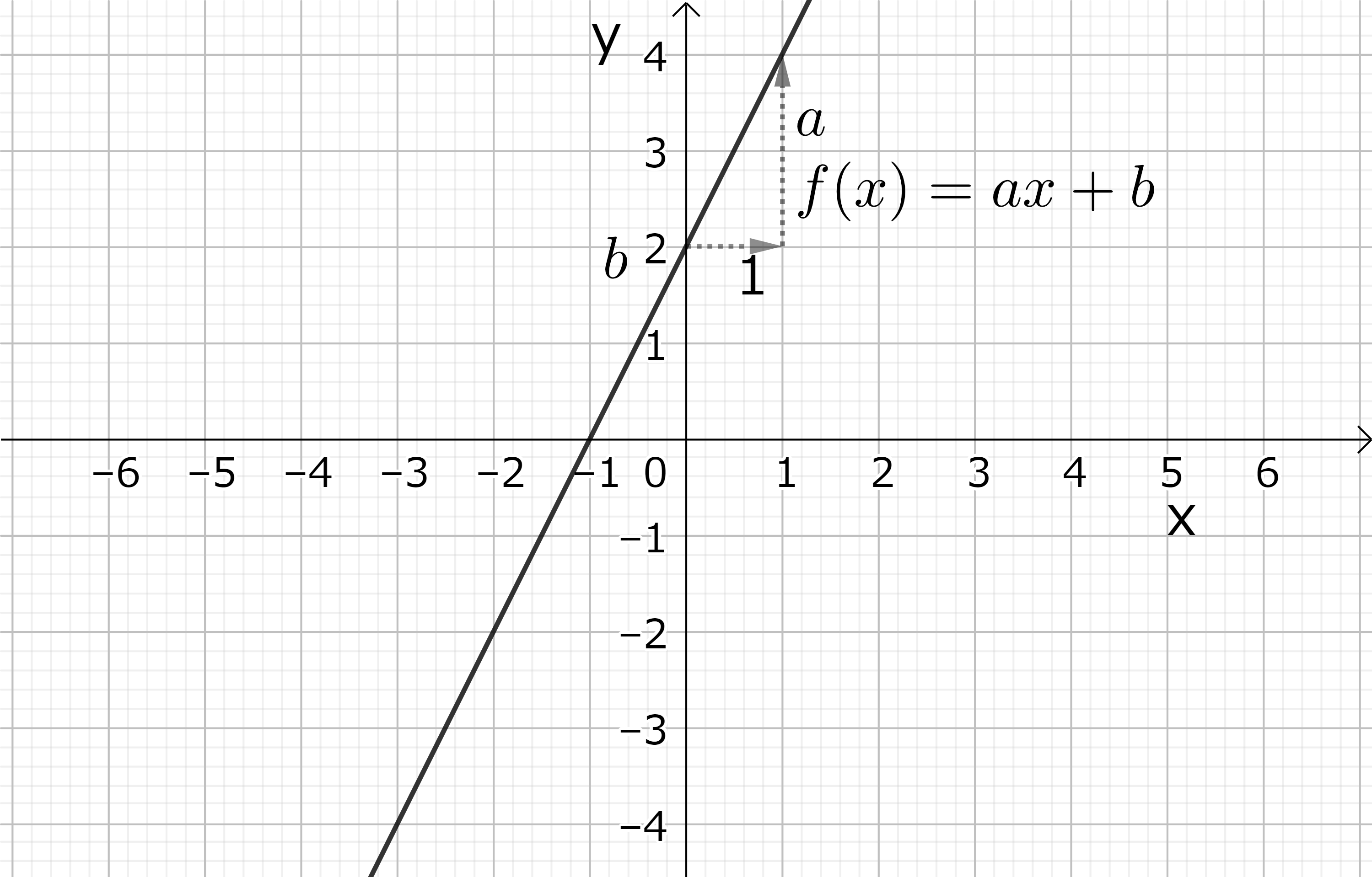
図4: \(y=ax+b \quad (a \neq 0) \) のグラフ。 \(a=2, b=2\) の場合
一次関数を表わす式は、必ずしも \( y=f(x) \) の形である必要はない。最も一般的な一次関数は \( ax+by+c=0 \) である。左辺を \(x\) と \(y\) の関数と考えて \( f(x,y)=ax+by+c \) として、\( f(x, y)=0 \) と表わす事も出来る。この様な関数の表わし方を隠伏関数 (あるいは、陰関数表示) と言う。もし \( b \neq 0 \) なら、 \( y=-\frac{a}{b} x-\frac{c}{b} \) と書き変える事により \( y=f(x) \) の形になる。 \( ax+by+c=0 \) の形は、\(x=0\) や \(y=0\) の場合を含む。即ち、\(x=0\) は \(y\)-軸を、\(y=0\) は \(x\)-軸を表わす。\( ax+by+c=0 \) は任意の 0 以外の数で割っても変わらないので、最も簡単な形にしておくことが得策である。例えば、 \(x\)-軸の切片 \(a (\neq 0)\), \(y\)-軸の切片 \(b (\neq 0) \) を通る直線は \( \frac{x}{a}+\frac{y}{b}=1 \) で表わされる。また、二点 P(\(x_0, y_0\) ) と P(\(x_1, y_1\) ) を通る直線のグラフは傾きが \( \frac{y_1-y_0}{x_1-x_0} \) だから
\[ y-y_0=\frac{y_1-y_0}{x_1-x_0} (x-x_0) \]
である。あるいは
\[ \frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0} \]
この式は、\( (x, y)=(x_0, y_0) \) の時 0=0、\( (x, y)=(x_1, y_1) \) の時 1=1 となっている。
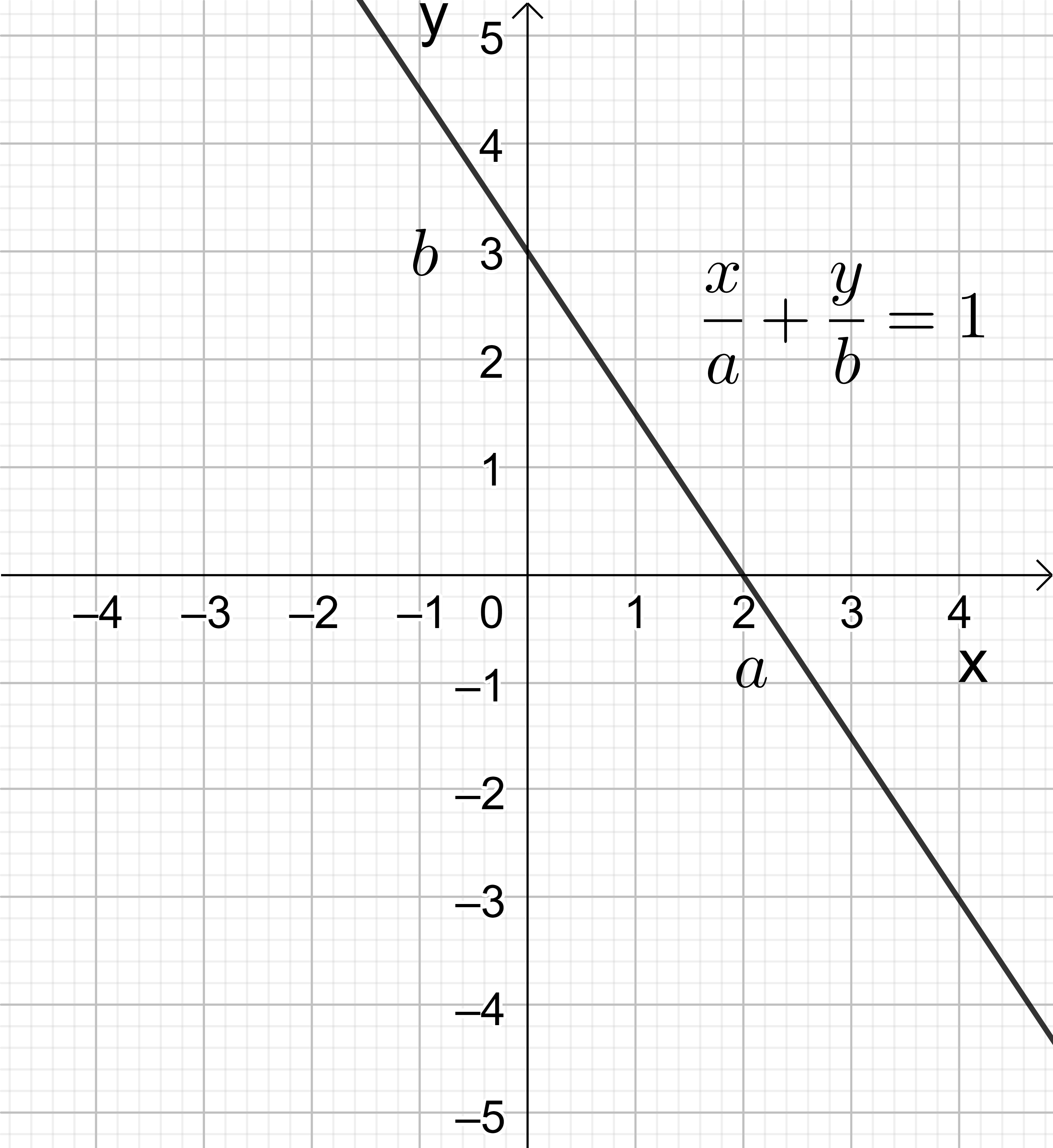
図5-1: 直線 \(\frac{x}{a}+\frac{y}{b}=1\) のグラフ
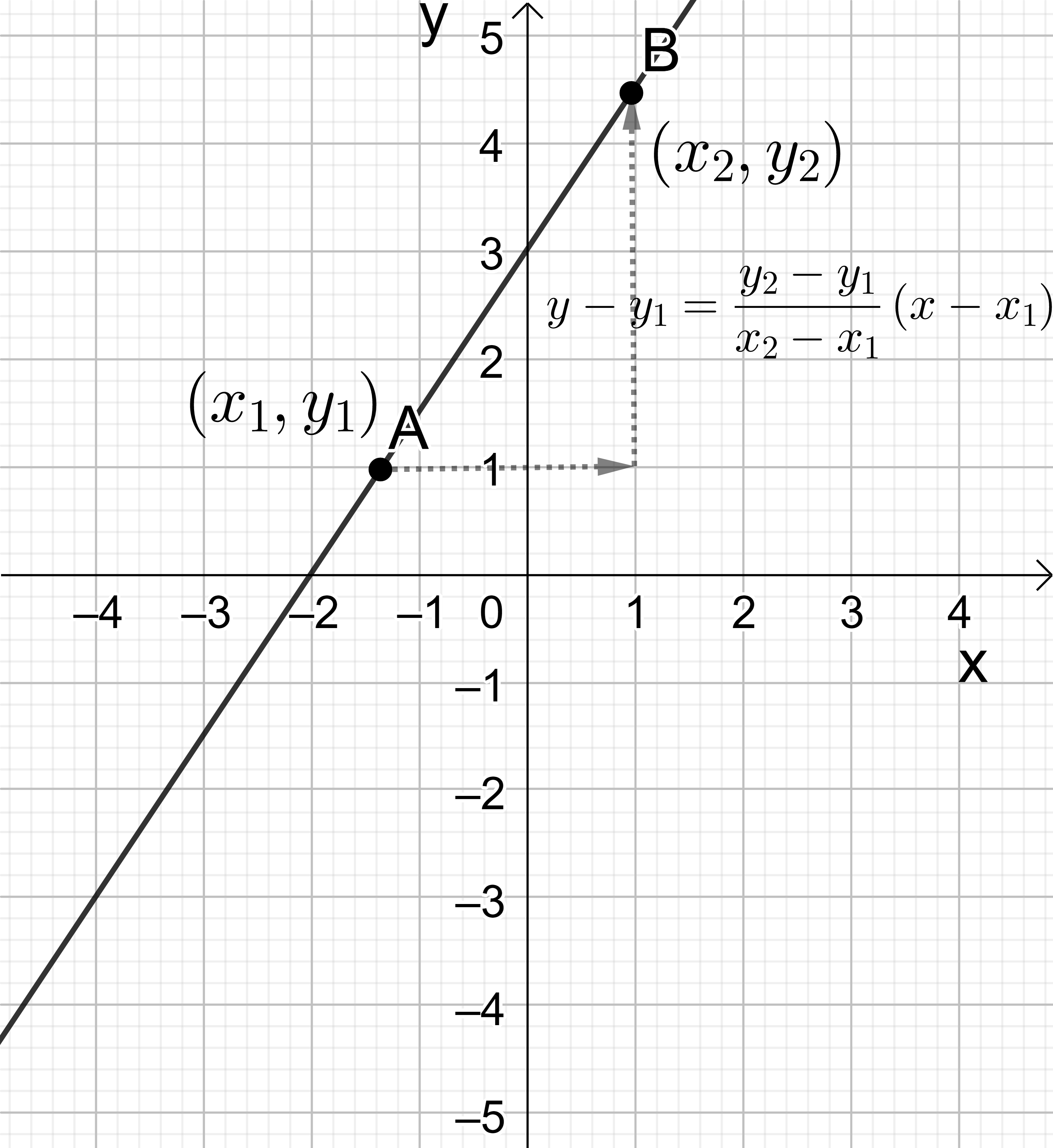
図5-2: 2 点 \(\hbox{A}(x_1, y_1), \hbox{B}(x_2, y_2)\) を通る直線のグラフ
.
二元連立一次方程式を解く事は、二つの直線の交点を求める事に対応している。例えば、2章で考えた鶴亀算では \( x+y=5\) と \(2x+4y=14 \) を表わす二つの直線の交点が P(3, 2) である事を示している。実際、方眼紙の上に \(x-y\) 座標を取り、\( \frac{x}{5}+\frac{y}{5}=1\) に対応する \(x\)-軸と \(y\)-軸の切片が 5 の直線を描き、更に \( \frac{x}{7}+\frac{y}{3.5}=1\) に対応する \(x\)-軸の切片 7、\(y\)-軸の切片 3.5 の直線を重ねると、\( (x, y)=(3, 2) \) で二つの直線は交わる。しかしながら、連立一次方程式は必ずしも常に解を持つとは限らない。例えば
\[ x+y=5 \\ 2x+2y=10 \]
という連立方程式は二つの式が同じ関係式、同じ直線を与えるので、交点は存在しない。この場合、方程式や解は不定と言う。また
\[ x+y=5 \\ 2x+2y=8 \]
ならば、二つの直線は互いに平行で決して交わらない。この場合、方程式は不能という。
\(a \) が 0 でない時 \( f(x)=ax^2+bx+c \ (a \neq 0) \) を二次関数という。一般的な一次関数 \( f(x)=ax+b \) を一意的に決定するためには、傾き \( a \) と\( y \)-軸の切片 \( b \) 等、最低限2つの定数 (これをパラメータという) が必要であるが、二次関数を一意的に決定するためには最低限3つの定数 \( a, b, c \) がいる。 一次関数では \(y=ax \) が基本的だった様に、二次関数では \( y=ax^2 \) が基本的である。しかし、今度は \( a \) は傾きではなしに、放物線が上に開いているか下に開いているかに関係している。すなわち、\( x \) が \( \pm \infty \) に近づく時に \( a >0 \) ならば \( y \) は \( \infty \) に、\( a < 0 \) であれば \( y \) は \( -\infty \) に近づく。\( y=ax^2 \) のグラフは \( y\)-軸に対して対称であり、放物線の頂点は座標の原点にある。
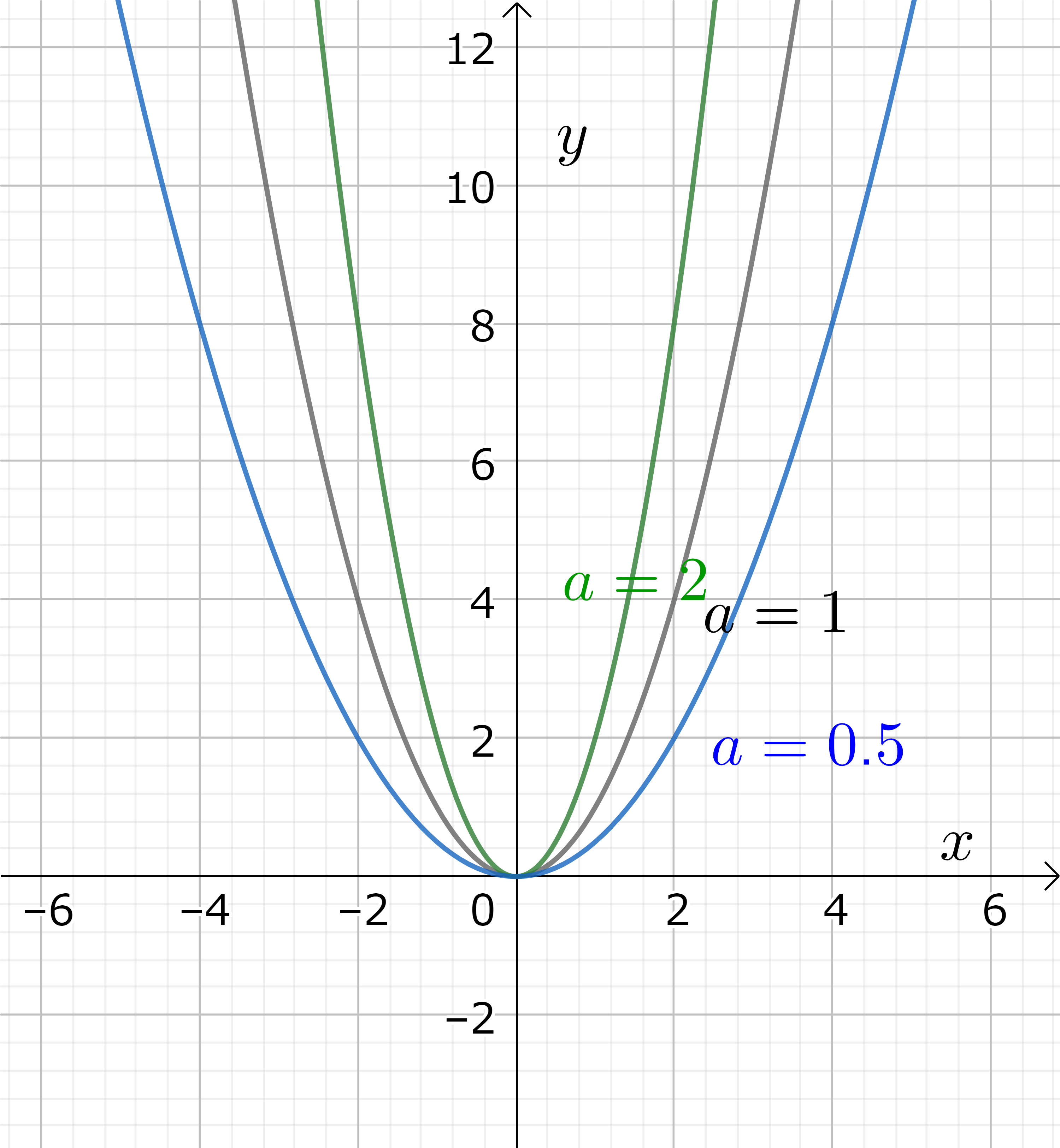
図6 (左): 2 次曲線 \(y=ax^2\) のグラフ。\(a > 0\) の場合
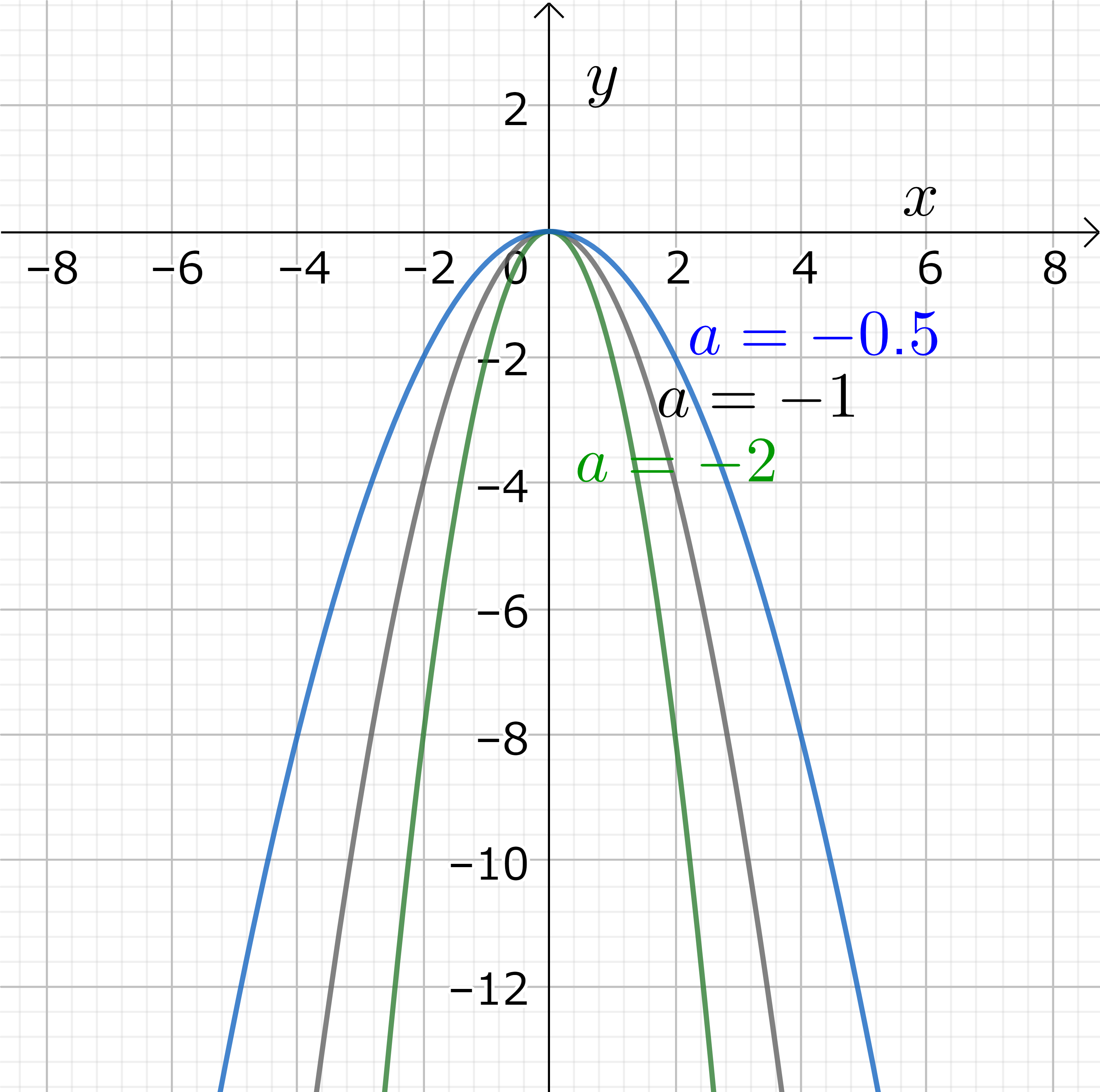
図6 (右): 2 次曲線 \(y=ax^2\) のグラフ。\(a < 0\) の場合
最も一般的な放物線 \( y=ax^2+bx+c \) のグラフを描くには、二次方程式のところで出て来た「完全平方」の形を用いるとよい。すなわち \[ y=a \left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a} \] これを \( y=a(x-x_0)^2+y_0 \) と書くと \[ x_0=-\frac{b}{2a} \quad , \quad y_0=-\frac{b^2-4ac}{4a} \tag{7-1} \] として \( (x_0, y_0) \) は放物線の頂点の位置である。また、グラフは \( x=x_0 \) の直線に関して左右対称である。上の式を \( y-y_0=a (x-x_0)^2 \) と表わすと、 \( y=a^2+bx+c \) は \( y=ax^2 \) を頂点が座標原点から \( (x_0, y_0) \) に移るように平行移動したものである。
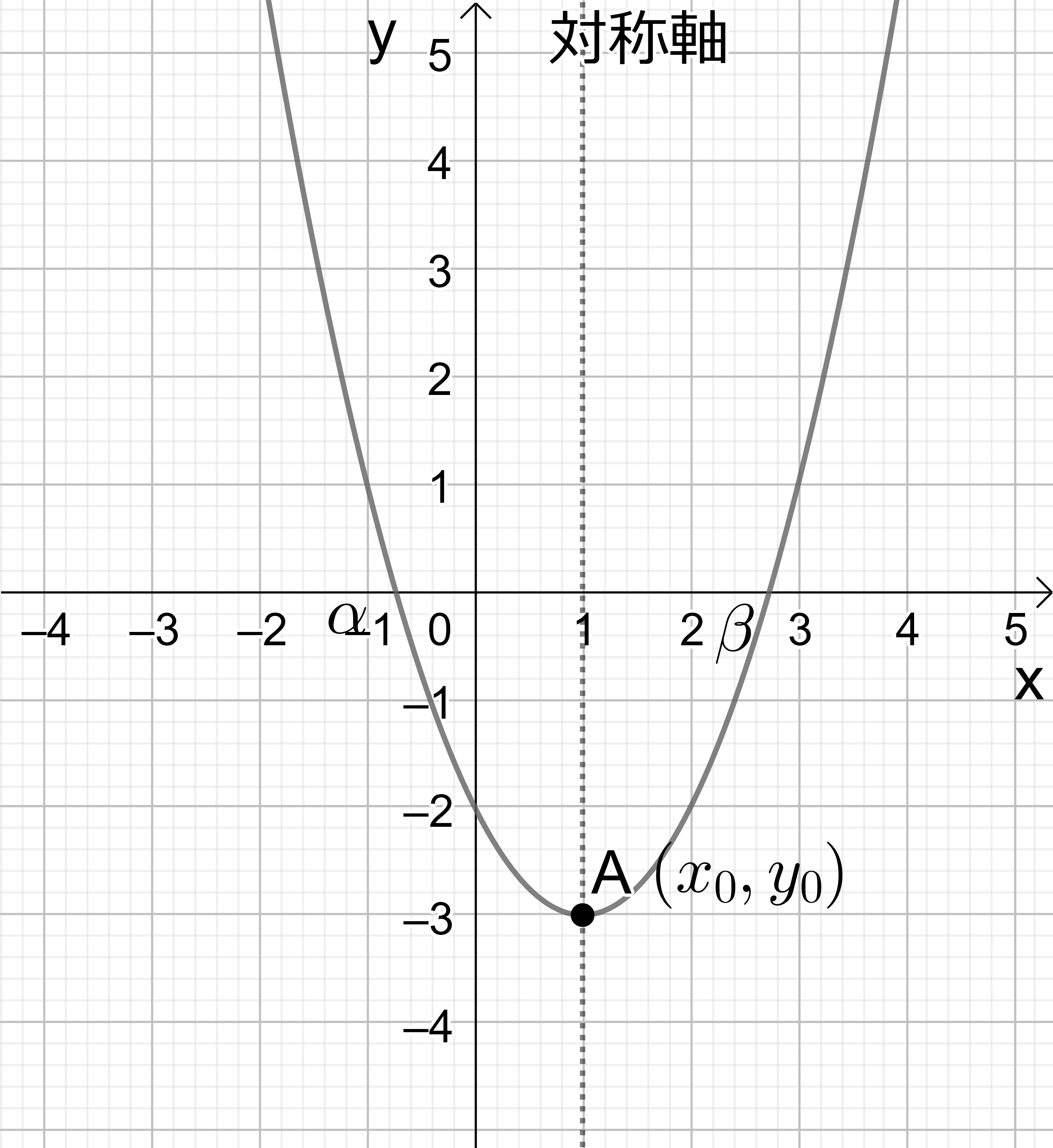
図7 (左): 2 次曲線 \(y-y_0=a(x-x_0)^2\) のグラフ。\(a > 0\) の場合
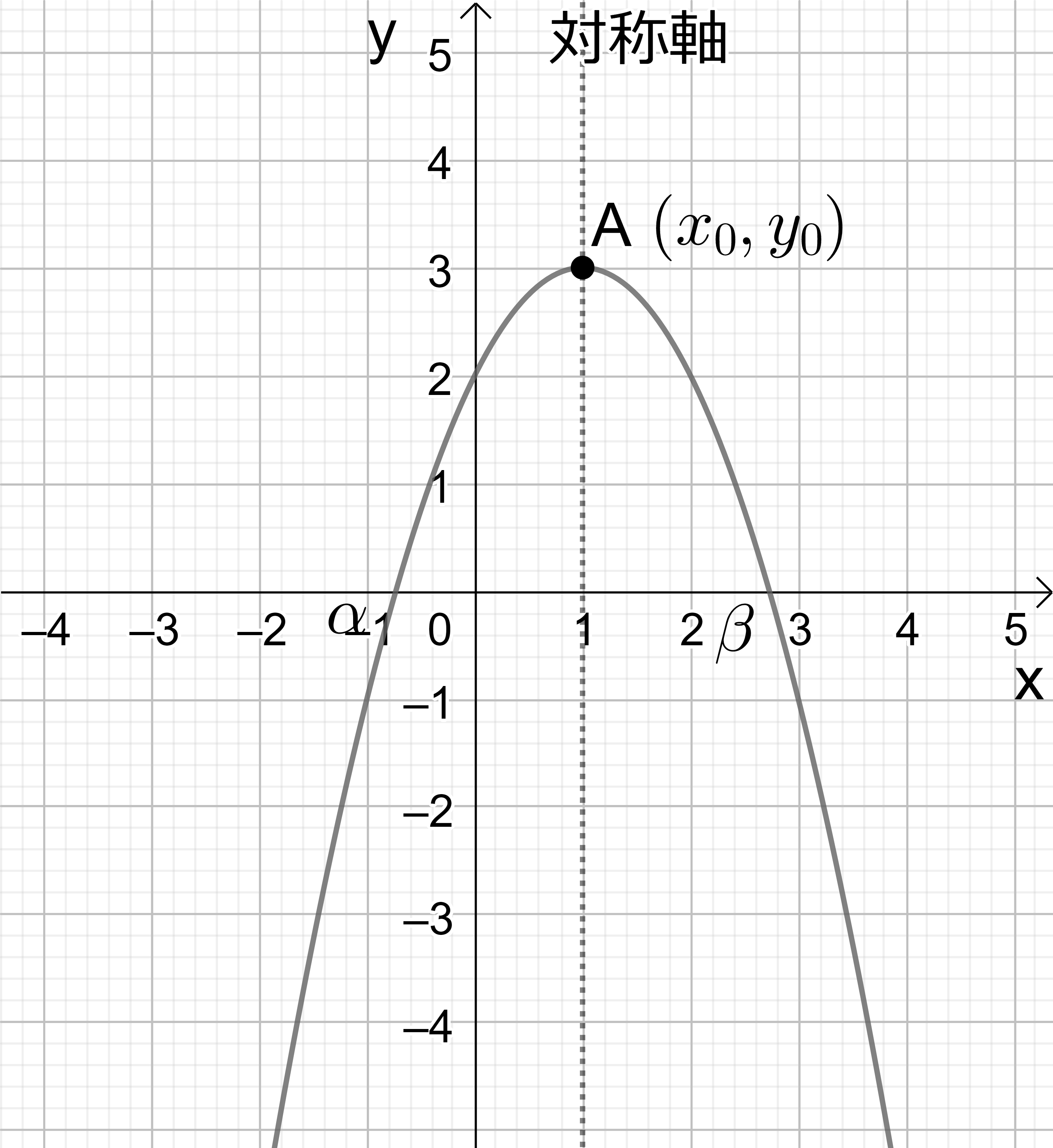
図7 (右): 2 次曲線 \(y-y_0=a(x-x_0)^2\) のグラフ。\(a < 0\) の場合
(追補-4) \( y=ax^2\) を\( ay=(ax)^2 \) と書いて、\( ay\) と \( ax\) を新しく
\( y\) と \( x\) と書く事により、\( y=ax^2\) のグラフは \( y=x^2 \) のグラフと相似である。( \( x\)-軸と\(y\)-軸の一様な拡大、縮小によって重ね合わせる事が出来る。) 最も一般的な放物線は \( y=ax^2 \) から平行移動によって得られるから、全ての放物線は \( y=x^2 \) のグラフの表わす放物線と相似である。この事は、後で見る様に、放物線が二次曲線といわれるグループの中で (離心率 \(e=1\) という) 非常に特殊なものである事に関係している。(円も非常に特殊で \(e=0\)である。)
頂点に替わるもう一つの放物線の特徴付けは二次方程式の解を使う方法である。 \( ax^2+bx+c=0 \) の二つの解を \( \alpha, \beta \) として、\( y=a(x-\alpha)(x-\beta) \) を再び完全平方の形に書くと
\[ y = a(x-\alpha)(x-\beta) \\ = a \left[ \left( x-\frac{\alpha+\beta}{2} \right)^2 -\left( \frac{\alpha-\beta}{2} \right)^2 \right] \]
となる。この式は右辺から左辺に和差の積の公式を適用する事によっても、簡単に証明できる。頂点の座標との関係は
\[ x_0=\frac{\alpha+\beta}{2} \quad , \quad y_0=-a\left( \frac{\alpha-\beta}{2} \right)^2 \]
である。この関係式から二次方程式の根と係数の関係を用いて (7-1) の結果が簡単に再現出来る。実際
\[ y_0 = -a \left[ \left( \frac{\alpha+\beta}{2} \right)^2-\alpha\beta \right] \\ = -a \left[ \left( -\frac{b}{2a} \right)^2-\frac{c}{a} \right] \\ = -\frac{b^2-4ac}{4a} = -\frac{D}{4a} \]
ここに、\( D=b^2-4ac \) は二次方程式の判別式である。ここから、\( D < 0 \) の時、\( a > 0 \) ならば上向の放物線は直交座標の上半平面にあり、\( a < 0\) ならば下向きの放物線が下半平面にあり、いずれも \( x\)-軸とは交わらないことが分かる。そこでこの場合は、二次方程式には実数解は存在せず、解は互いに複素数共役な二つの複素数解が存在することが分かる。
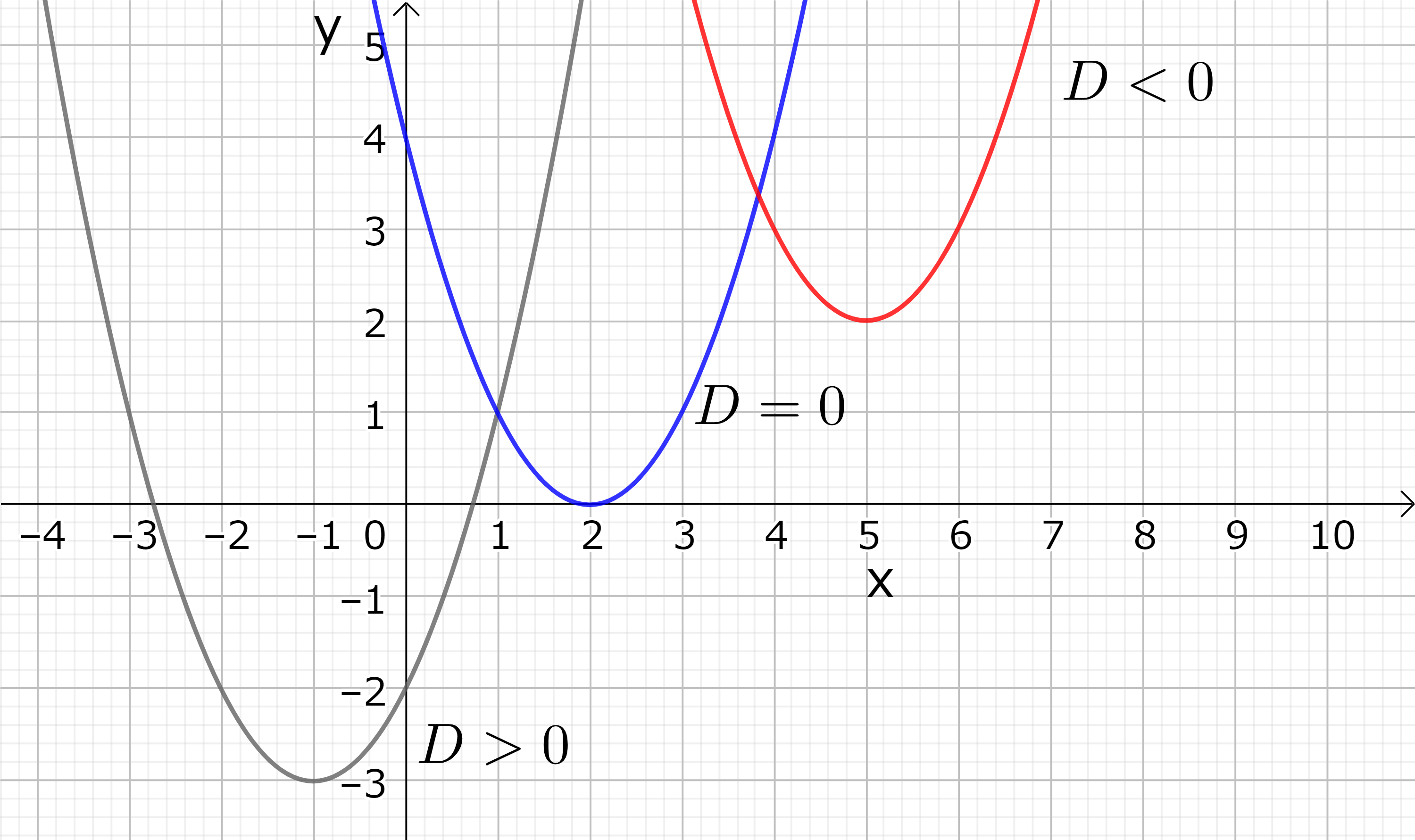
図8 (左): \(D > 0, D=0, D < 0\) の二次曲線 (放物線) のグラフ。\(a > 0\) の場合
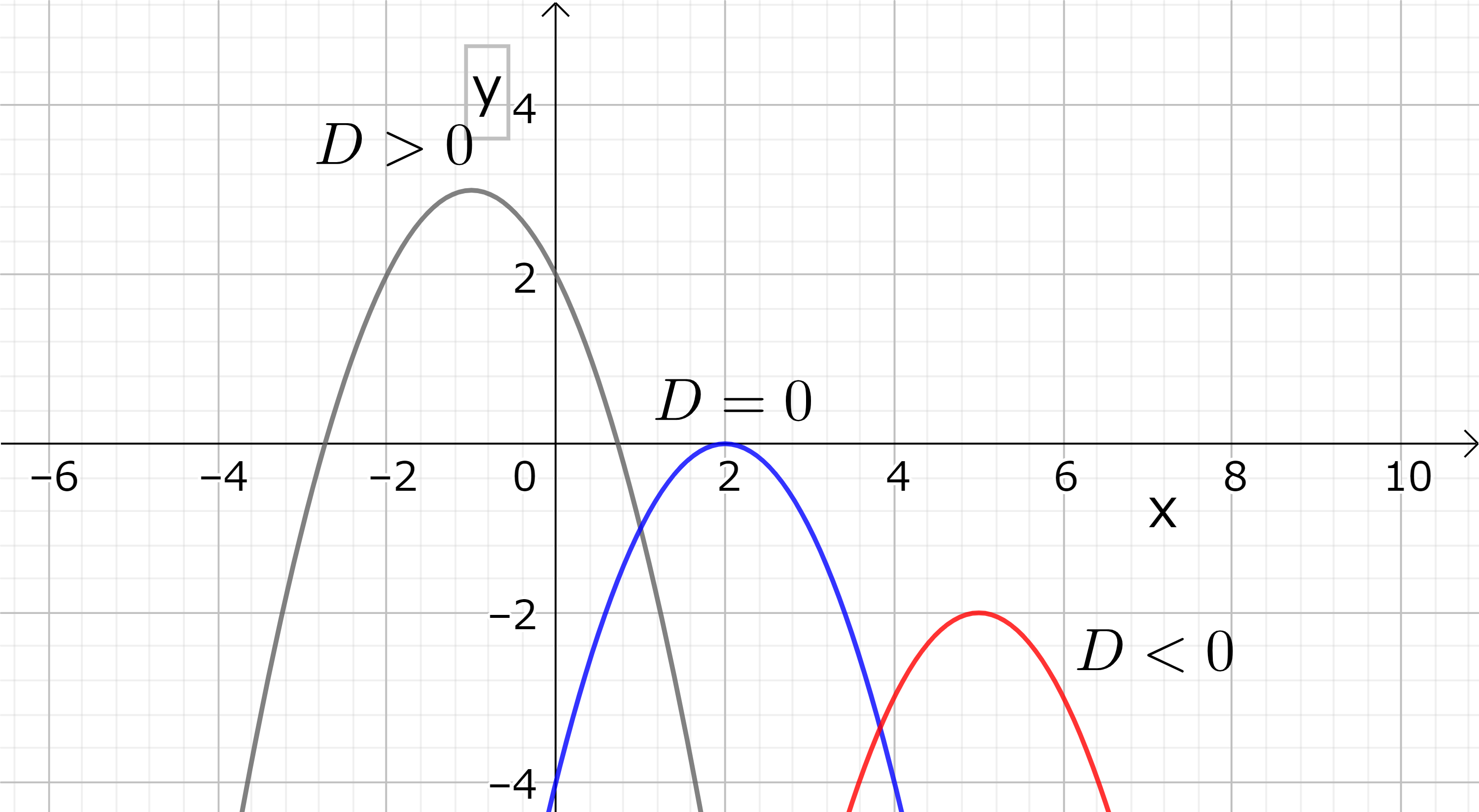
図8 (右): \(D > 0, D=0, D < 0\) の二次曲線 (放物線) のグラフ。\(a < 0\) の場合
実数係数を持つ3次以上の関数についても、そのグラフの様子より対応する「代数」方程式の解の大体の性質を知ることが出来る。例えば、3次関数で基本的なのは \( y=ax^3 \ (a \neq 0) \) であるが、この関数のグラフは \( x \rightarrow \pm \infty \) の時 ( \( a\) の符号によるが) 互いに反対方向の \( \pm \infty \) に発散する。このことは、一般の三次函数 \( y=ax^3+bx^2+cx+d \ (a \neq 0) \) についても同様である。( \(x^3\) の項が主要な項となるからである。) 従って、実数係数の三次方程式 \( ax^3+bx^2+cx+d=0 \ (a \neq 0) \) は必ず実数解を一つ持つ。この解を \( x_0\) とすると、左辺の三次式は必らず \( (x-x_0) \) で割り切れるから、残りの二次方程式は判別式の符号に応じて (重根を含めて) 二つの実数解か互いに複素共役な二つの複素数解を持つ。これらを \( x_1, x_2 \) とすると三次函数は
\[ y= ax^3+bx^2+cx+d=a(x-x_0)(x-x_1)(x-x_2) \]
と因数分解される。
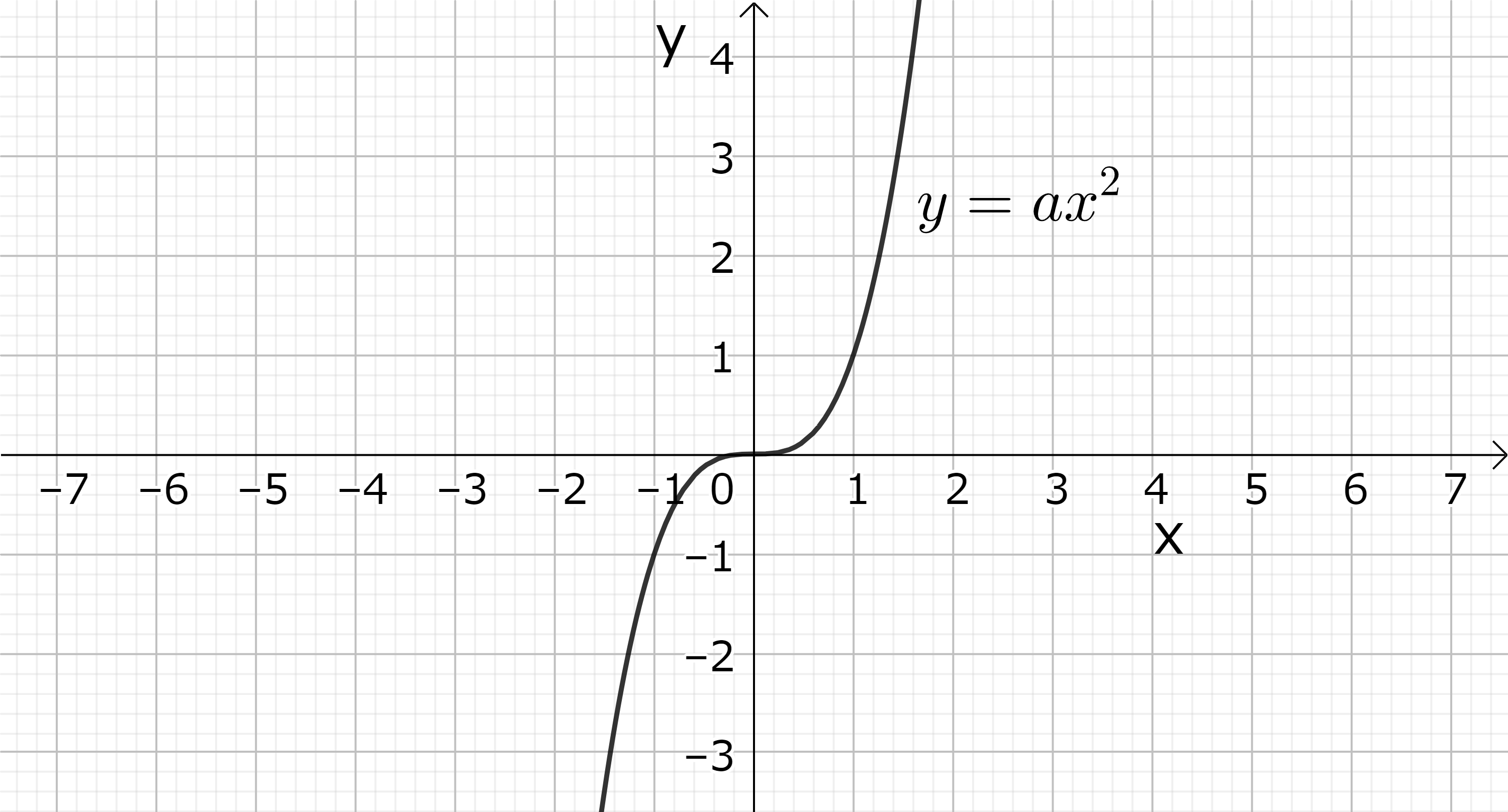
図9 (左): 最も簡単な三次関数 \(y=a^3\)、 \(a > 0\)
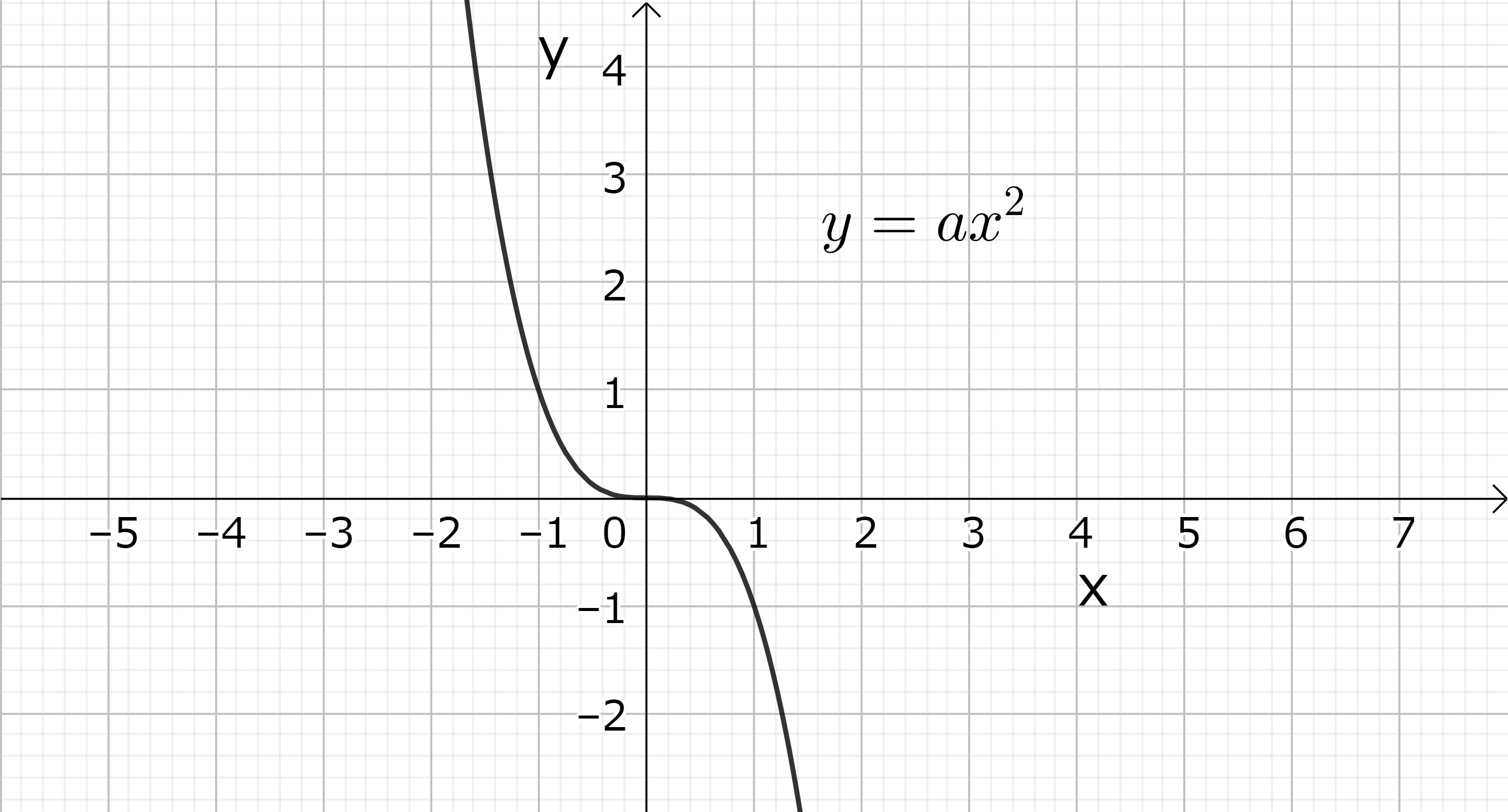
図9 (右): 同左、ただし \(a < 0\)
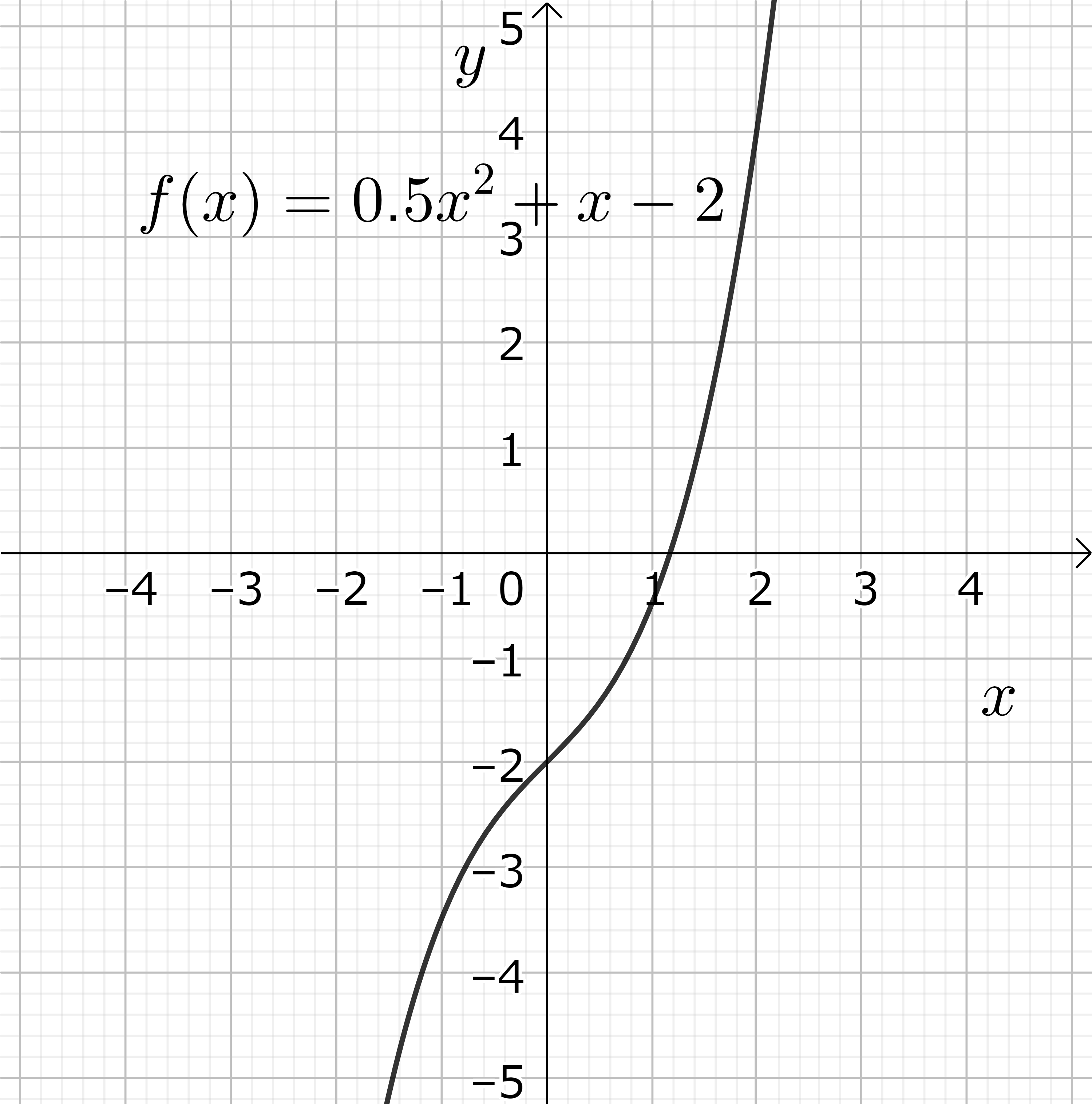
図10 (左): 三次関数の例-1、\(y=0.5x^3+x-2\)
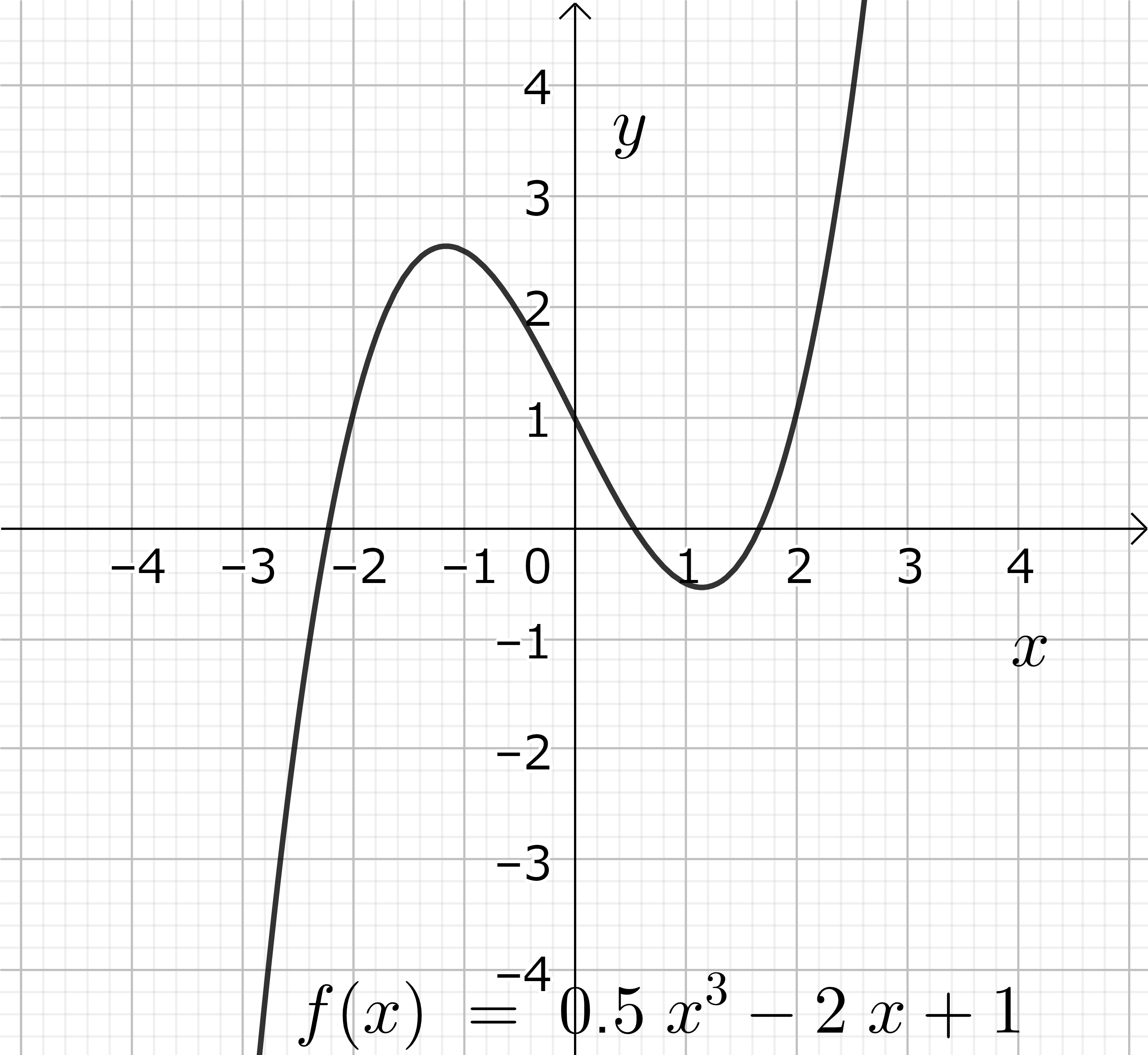
図10 (右): 三次関数の例-2、\(y=0.5x^3-2x+1\)
.
直交座標上の二点間の距離、円の方程式、極座標表示、一般角、ラジアン、三角関数
2次元直交座標系の2点 P(\(x, y\) ), Q(\(x',y'\) ) 間の距離 \( \ell \) は、ピタゴラスの定理を使って
\[ \ell = \sqrt{(x-x')^2+(y-y')^2} \]
により求められる。特に P 点の原点からの距離 \( r\) は、\( r=\sqrt{x^2+y^2} \) である。そこで
\[ x^2+y^2=r^2 \]
を満たす点 P(\(x,y\) ) の全体は原点を中心とする半径 \(r\) の円を表わすことが分かる。 また、Q\((x_0, y_0)\) を中心とする半径 \(r\) の円は
\[ (x-x_0)^2+(y-y_0)^2=r^2 \]
と表わされる。
P 点と原点を結んだ線分が \(x\)-軸の正の半直線から (反時計回りに) 測った角度を \( \theta \) とすると、P 点を表わすのに直交座標 \( (x, y) \) の代わりに \( (r, \theta ) \) の組みを取ることも出来る。これを極座標といい、\(r\) を極座標の動径部分、\( \theta \) を角度部分、P\( (r, \theta ) \) を P 点の極座標表示という。(もとの P(\(x, y\)) は直交表示という。) \(x\) と \(y\) の値は \( -\infty \) から \( \infty \) の全ての値をとるが、\(r\) の可能な値は 0 から \( \infty \) だけである。一方、角度部分に対しては、\(x\)-軸の正方向を 0 として左回りに 0 から \( \infty \), 右回りに 0 から \( -\infty \) としておくと都合が良い。これを一般角という。角度を測る単位としては、小学校以来直角を90度 (90°) とし円周を360度 (360°) とするのが一般的であるが、これは60進法の名残りである。より理論的には、円弧の長さを円の半径を単位として測った、いわゆるラジアン ( radian) がよく使われる。円周の長さは \( 2 \pi r \) だからこれを半径 \(r\) で割ると、\( 360°=2\pi\) radian である。ラジアンは無単位なので、普通 radian は省略する。そこで、360°=2π、90°=π/2 である。逆に 1 radian = 180°/π = 57.2957... °である。角度を反時計回り (counterclockwise) に測るのは単なる習慣である。
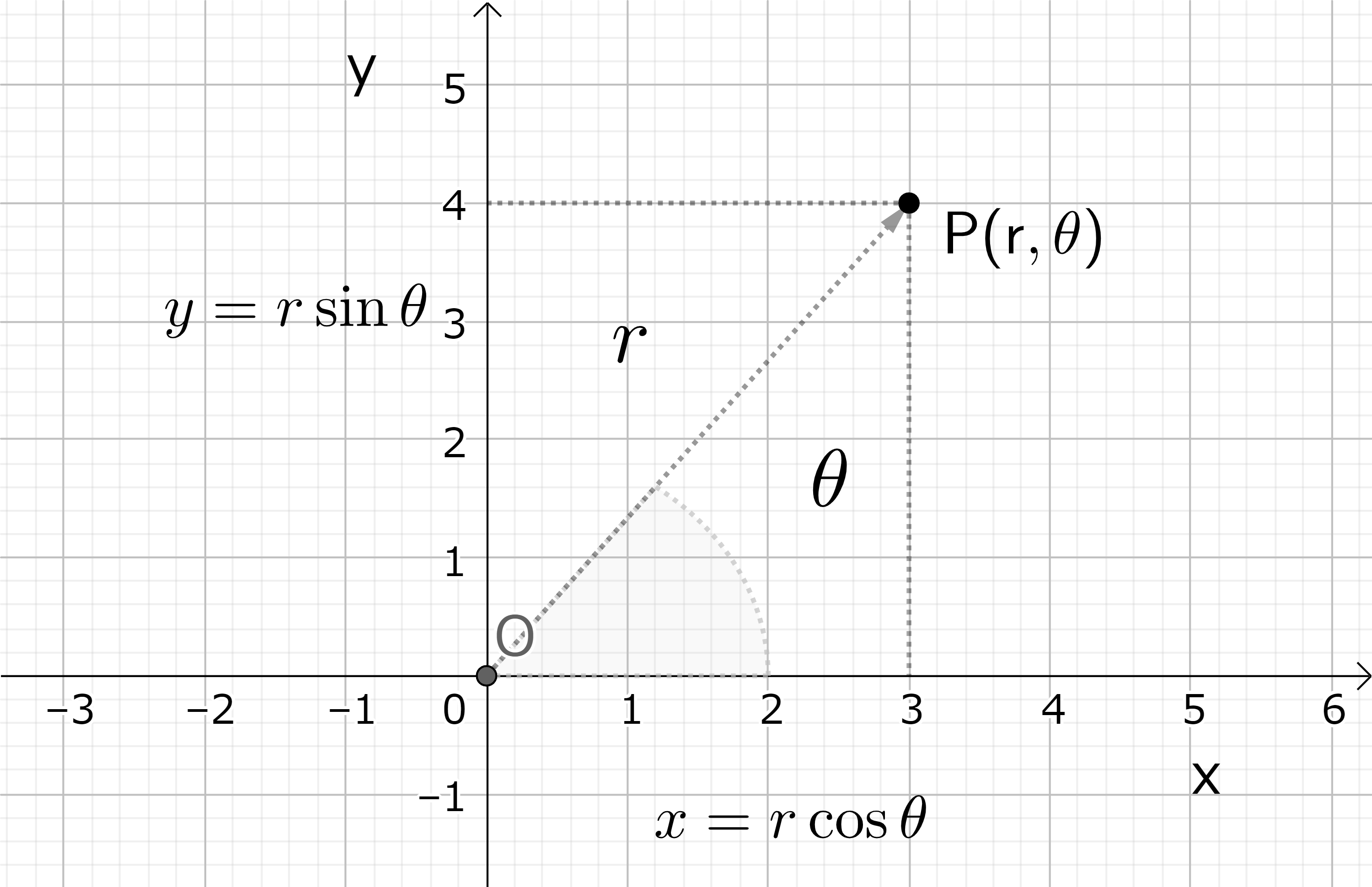
図11: 直交表示と極座標表示
三角関数 sine, cosine を使うと直交表示と極座標表示との間の関係を簡単に表わすこと が出来る。すなわち
\[ x=r \cos \theta\ , \quad y=r \sin \theta \]
ここに、\( x^2+y^2=r^2 \) は \( (\cos \theta)^2+(\sin \theta)^2=1 \) に対応する。
(追補-5) 直交座標系における二点間の距離の簡単な応用例として、アポロニウスの円がある。まず、\(x\)-軸上に \( -a\) と \( b\) の二点を取り( \( a>0, b>0 \) と仮定する) この二点からの距離の比が \( a : b\) となる様な点 P(\(x, y\) ) 全体の集合を考える。座標原点はもちろん、その様な集合に含まれる。もし、\( a=b \) なら \(y\)-軸がその様な点全体の集合になる事は明らかである。(二等辺三角形である。) 一般の場合には
\[ \sqrt{(x+a)^2+y^2} : \sqrt{(x-b)^2+y^2}=a : b \]
より
\[ a \sqrt{(x-b)^2+y^2} = b \sqrt{(x+a)^2+y^2} \]
これを2乗して式を整理すると
\[ a^2 [(x-b)^2+y^2] = b^2 [(x+a)^2+y^2] ,\\ a^2 (x^2-2bx+b^2+y^2) = b^2 (x^2+2ax+a^2+y^2) ,\\ (a^2-b^2)(x^2+y^2) = (2a^2 b+2a b^2)x ,\\ (a+b)(a-b)(x^2+y^2) = 2ab(a+b)x \]
ここに \( a, b, a+b >0 \) より\( a+b\) で割ると
\[ (a-b)(x^2+y^2) = 2abx \]
そこで、もし \( a=b \) なら \( x=0 \) で、この式は y-軸を表わす。逆に \( a\neq b\) なら、\( a-b \) で割って式を整理すると
\[ x^2-2\frac{ab}{a-b} x+y^2 = 0 ,\\ \left(x-\frac{ab}{a-b}\right)^2+y^2 = \left(\frac{ab}{a-b}\right)^2 \]
この式は \(x\)- 軸上の点 \( x=\frac{ab}{a-b} \) に中心を持つ半径 \( \vert \frac{ab}{a-b}\vert \) の円を表わす。この円はもちろん座標原点を通る。これをアポロニウスの円という。\( a → b\) とすると円の半径は益々大きくなり、ついには \(y\)-軸と一致する。アポロニウスの円は、平行線と交わる直線の公理と三角形の相似比を使っても初等的に導くことが出来る。(幾何分野の項、参考)
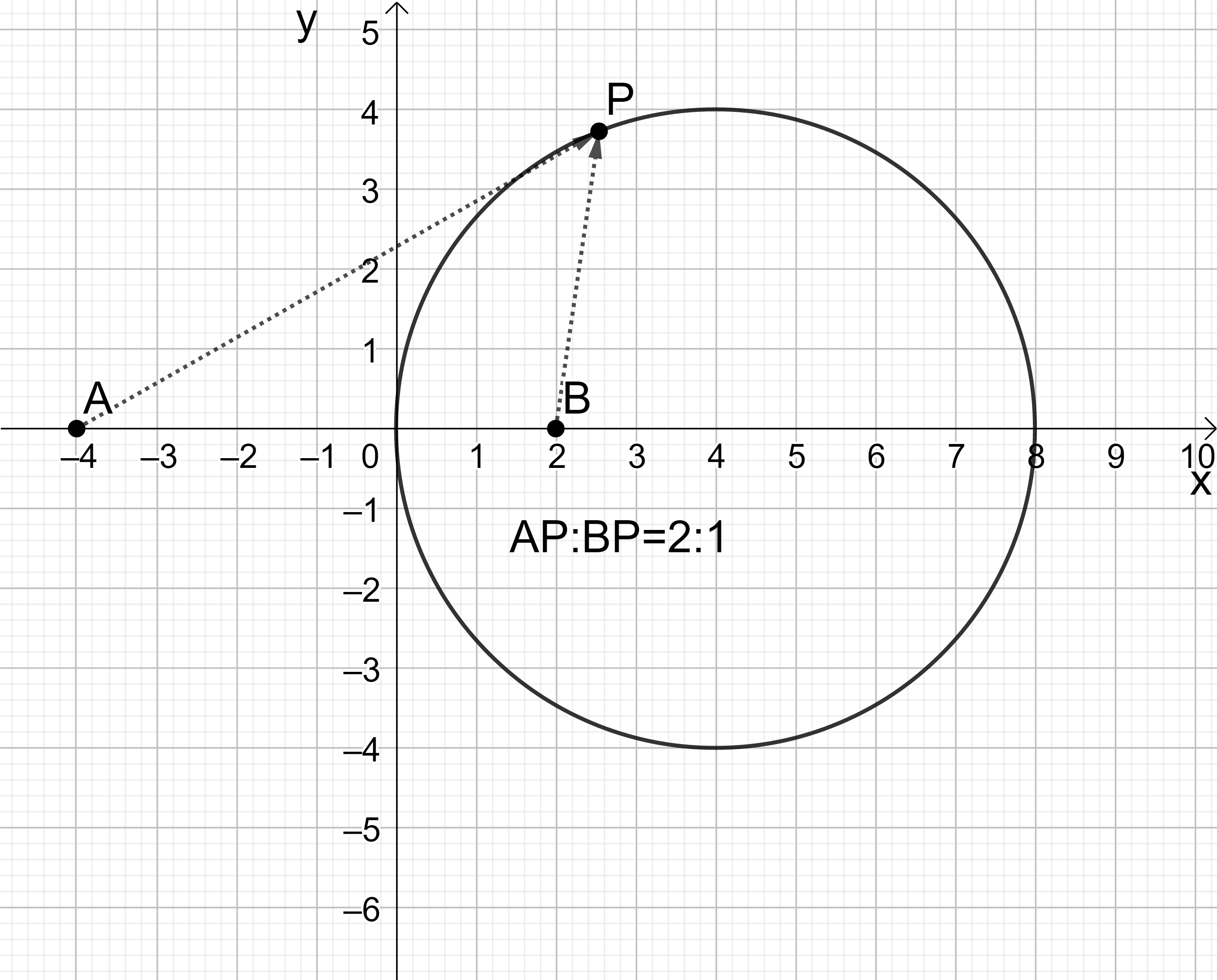
図12 (左): アポロニウスの円、\(|a| > b\) の場合
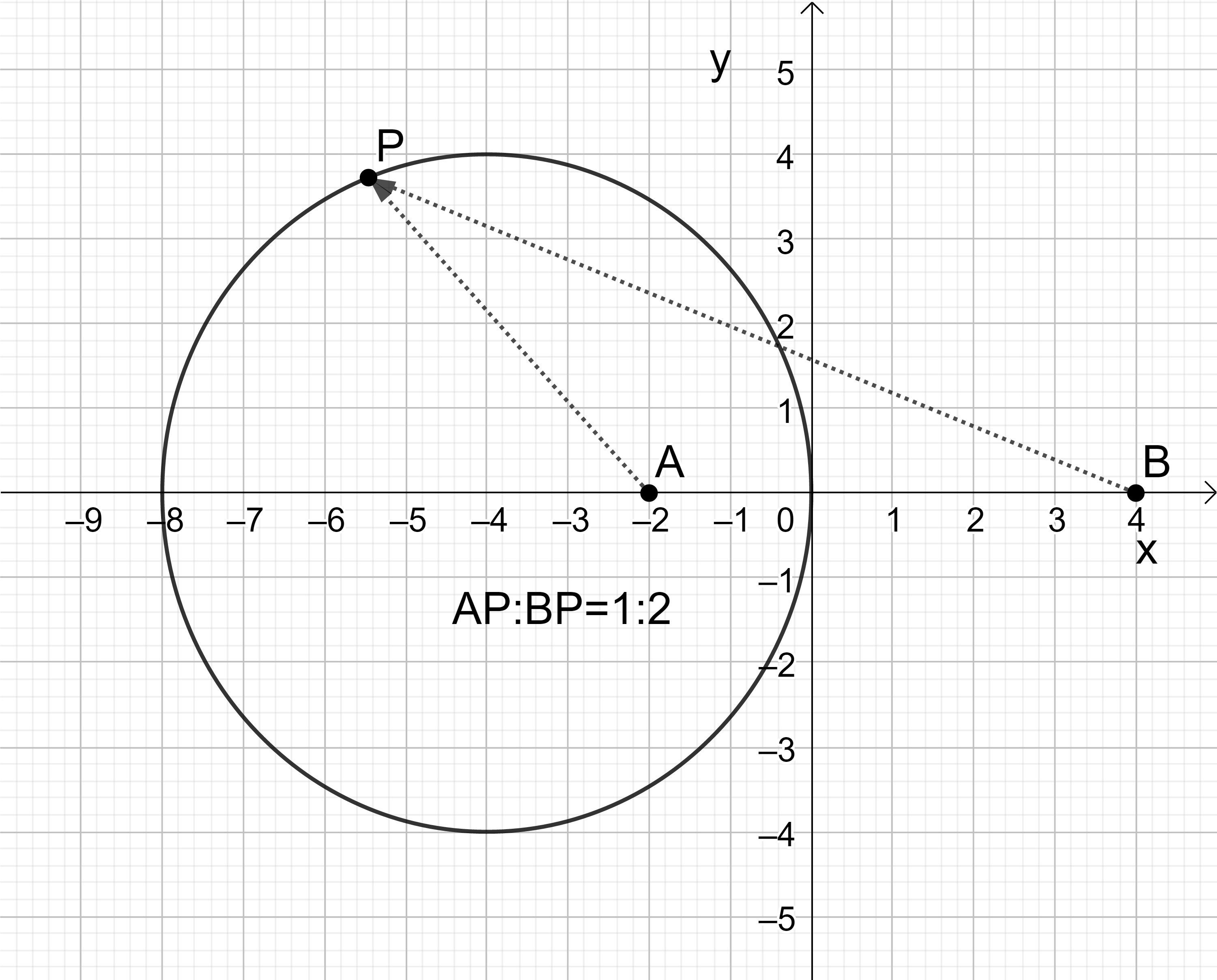
図12 (右): アポロニウスの円、\(|a| < b\) の場合
.
二次曲線
円、楕円、放物線、双曲線を総称して二次曲線 (円錐曲線とも言う) といい、統一的な取り扱いが可能である。最も一般的には、これらはいずれも \(x\) と \(y\) の二次関数 \( f(x, y) \) を 0 と置いた隠伏関数表示で表わされる。まずはじめに、 \(x\)-軸、\(y\)-軸のそれぞれについて対称な最も簡単な楕円と双曲線について考えよう。
楕円は原点を中心とする半径 \(r\) の円の方程式 \( x^2+y^2=r^2 \) を拡張して
\[ \left( \frac{x}{a}\right)^2+\left( \frac{y}{b}\right)^2=1 \tag{9-1} \]
として得られる。(図13-1参照) 今 \( a > b \) と仮定して \( a\) を長径、\( b\) を短径という。 それらが共通の値 \( r\) ではないのである。これに伴って楕円の "中心" も二つあって、それを楕円の焦点という。\(e\) という \(0 < e <1\) のパラメータ (離心率という) を新たに導入して、\(x\)-軸上の \(-ea\) と \(ea\) に焦点を置く。楕円はこれらの焦点からの距離の和が \( 2a\) となるという条件によって特徴付けられる。 特に \( x=0\) の時、楕円 (9-1) の上の点 P の座標 P(0, \(b\)) の値は二つの焦点と原点、および P 点を結ぶ二つの直角三角形を考えることにより
\[ b=\sqrt {a^2-(ea)^2}=a\sqrt{1-e^2} \tag{9-2} \]
である事が分かる。\( e=0, a=b=r \) が円の場合である。 点 P(\(x, y\)) の二つの焦点からの距離の和が \( 2a\) であるという条件は
\[ \sqrt{(x+ea)^2+y^2}+\sqrt{(x-ea)^2+y^2}=2a \]
と表わされる。これを変形すると、上の楕円の式が得られる。実際、左辺二項目の式を右辺に移行して2乗を取ると
\[ (x+ea)^2+y^2=(x-ea)^2+y^2+4a^2-4a \sqrt{(x-ea)^2+y^2} ,\\ 4a \sqrt{(x-ea)^2+y^2}=4a^2-4eax=4a(a-ex) ,\\ \sqrt{(x-ea)^2+y^2}=a-ex ,\\ (x-ea)^2+y^2=(a-ex)^2=a^2-2eax+e^2 x^2 ,\\ (1-e^2)(x^2-a^2)+y^2=0 ,\\ \left( \frac{x}{a}\right)^2+\left( \frac{y}{a\sqrt{1-e^2}}\right)^2=1 ,\\ \left( \frac{x}{a}\right)^2+\left( \frac{y}{b}\right)^2=1 \]
となる。最後の部分では \( b=a\sqrt{1-e^2}\) を使った。\( x=ea\) に楕円の中心を移すと、そのグラフを表わす方程式は平行移動の原理から
\[ \left( \frac{x-ea}{a}\right)^2+\left( \frac{y}{b}\right)^2=1 \tag{9-3} \]
となる。二次曲線の極座標表示は、一つの焦点 (ここでは右の焦点を取ることにする) を座標原点に選ぶ事により簡単になる。(図13-2 参照) すなわち、(9-1) の方程式で \( x=ea+ r \cos \theta, y=r \sin \theta \) と置くことにより
\[ \left( \frac{ea+r \cos \theta}{a}\right)^2+\left( \frac{r \sin \theta}{a\sqrt{1-e^2}}\right)^2=1 \tag{9-4} \]
が得られる。この式を簡単にすることにより
\[ r=\frac{d}{1+e \cos\ \theta} \tag{9-5} \]
が得られる。ここに、\( d \) は (9-1) で \( x=ea \)とした時の \(y\) の値の絶対値 \( |y|=b\sqrt{1-e^2}=a(1-e^2) \)から
\[ d=a(1-e^2) \tag{9-6} \]
と求められる。((9-5) における \( \theta=π/2 \) の時の \(r\) の値である。) この点 Q のもう一つの焦点からの距離は直角三角形に対するピタゴラスの定理から
\[ \sqrt{(2ea)^2+a^2(1-e^2)^2}=a(1+e^2) \]
であるので、二つの焦点から測った点 Q までの距離の和は再び \( a(1+e^2)+a(1-e^2)=2a \) となる。(9-4) から (9-5) を導くにはかなりの忍耐が必要であるが、次の様にして求められる。まず
\[ \left( \frac{r}{a}\right)^2 \left( (\cos \theta )^2+\frac{(\sin \theta)^2}{(1-e^2)}\right)+\frac{2er}{a} \cos \theta = 1-e^2 \]
ここで両辺に \( a^2(1-e^2) \) を掛けると
\[ r^2 (1-(e\cos \theta)^2)+2a(1-e^2) er\cos \theta=(a(1-e^2))^2 \]
ここで (9-6) の \( d\) を使うと
\[ r^2=(er\cos \theta)^2-2der\cos \theta +d^2=(d-er\cos \theta)^2 \]
そこで \( r=\pm (d-er\cos \theta) \) であるが、\( r\cos \theta \) の最大値は \( a(1-e) \) であるので
\[ d-er\cos \theta > a(1-e^2)-ea(1-e)=a(1-e) >0 \]
一方、\( r > 0 \) なので \( \pm \) のうち \(+\) だけが可能であり \( r=d-er\cos \theta \) つまり\( r(1+e\cos \theta)=d \) より (9-5) が成り立つ。
(9-5) 式は多少変形する事により、楕円のもう一つの特徴付けを与える。すなわち (9-5) を
\[ r : \frac{d}{e}-r \cos \theta = e : 1 \tag{9-7} \]
と書くと、この式は点 P の極座標表示 P\( (r, \theta)\) で座標原点と直線 \( x=\frac{d}{e} \) までの距離が \( e : 1 \)の比である事を表わす。(図13-2)
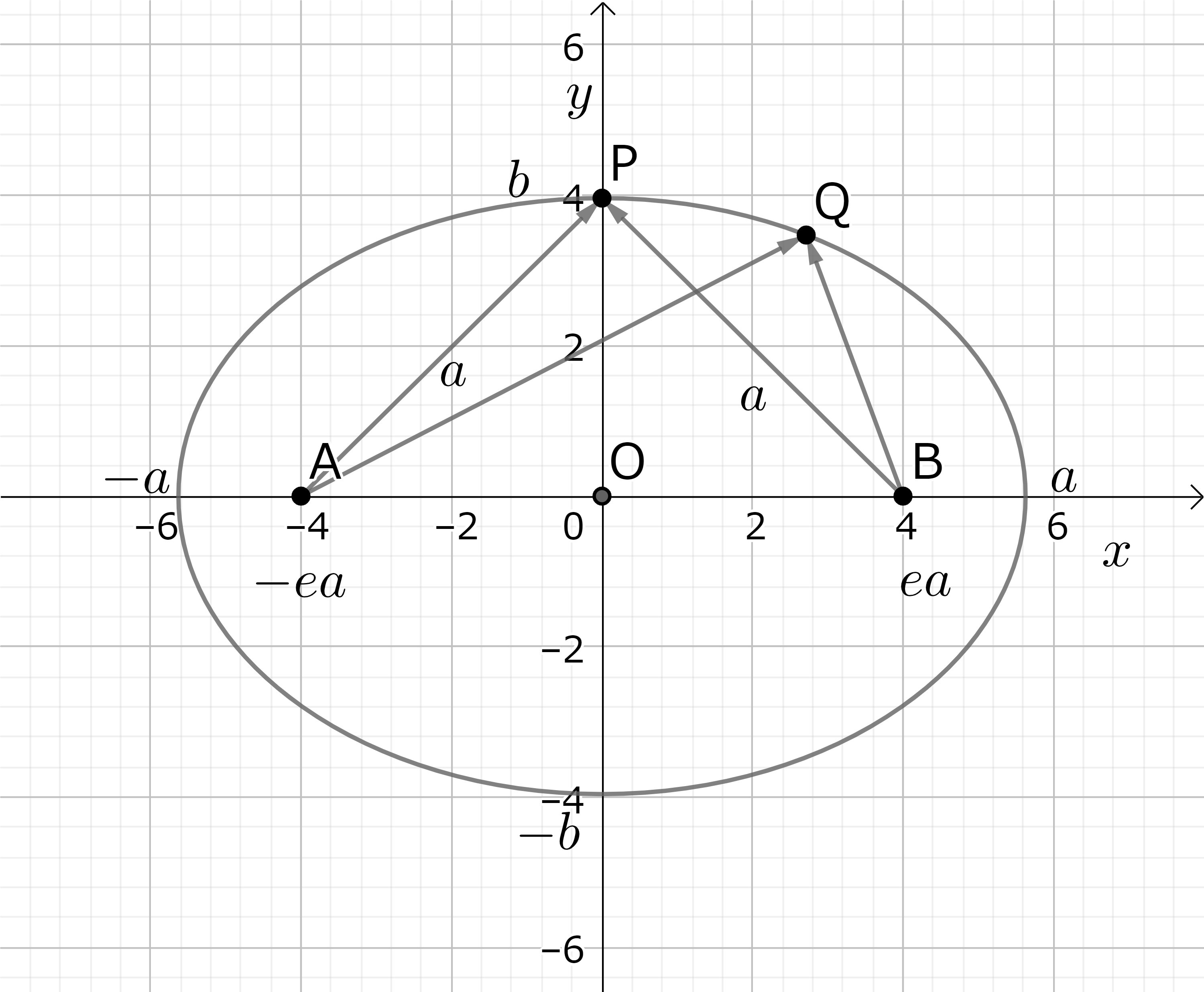
図13-1: 楕円、直交表示
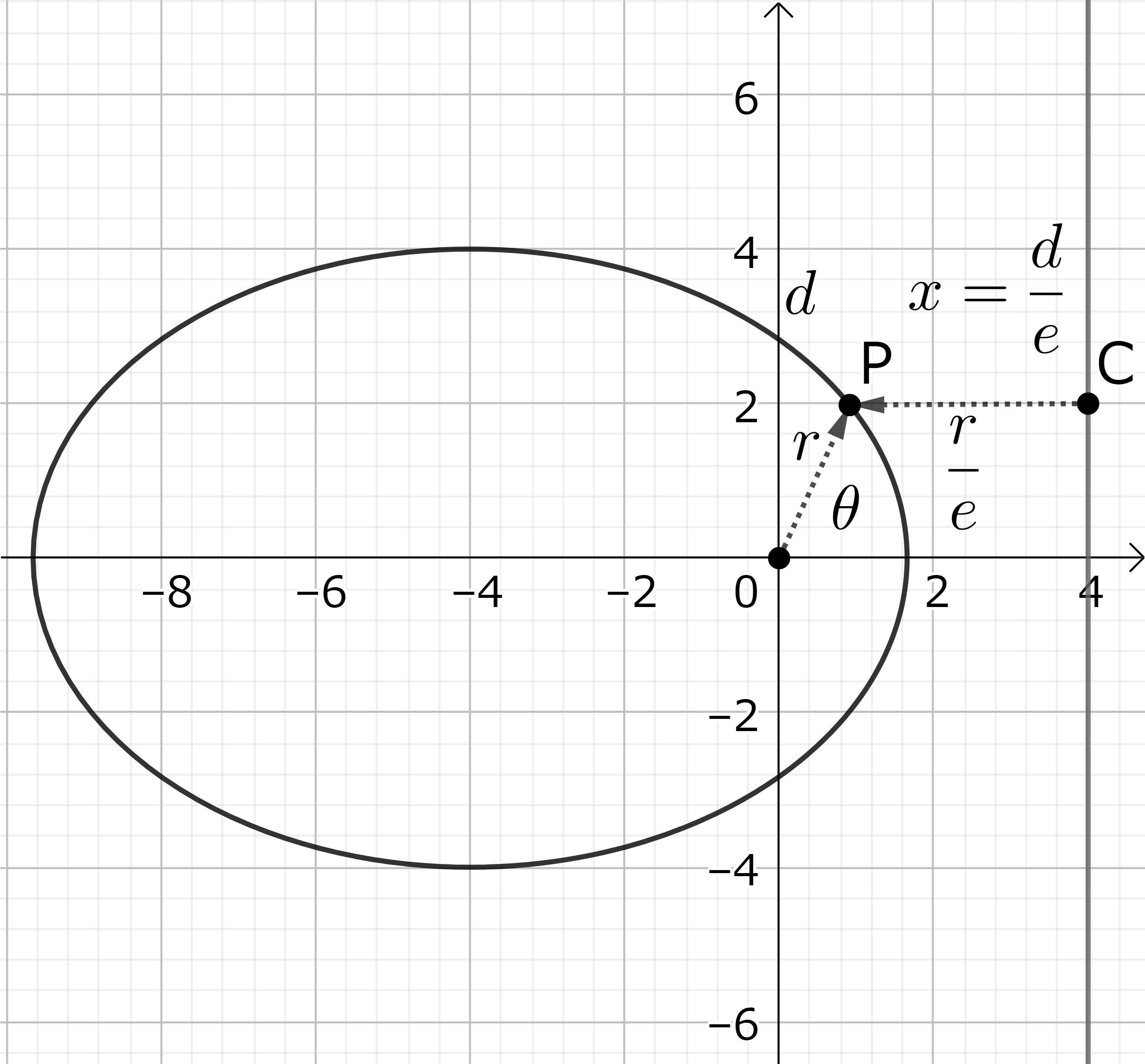
図13-2: 楕円、極座標表示
実は (9-5) 式は二次曲線を極座標で表わす一般的表式で、パラメータ \(e\) はそれぞれ
\[ e=0 : 円 \\ 0 < e < 1 : 楕円 \\ e=1 : 放物線 \\ e > 1 : 双曲線 \tag{9-8} \]
の領域に存在する。\(e → 0 \) の極限では、円の右に存在する直線は \( x → \infty \) に移ると考える。\(e=1\) の時の放物線は \(x\)-軸と\(y\)-軸をひっくり返して、\(y\)-軸上の \( y=d/2 \) に焦点を、\( y=-d/2 \) に直線を取ると考えやすい。点 P の直交表示 P(\(x, y\)) から焦点と直線までの距離を等しいとおくと
\[ \sqrt{x^2+(y-d/2)^2}=|y+d/2| \]
が得られる。これを2乗して、簡単に
\[ y=\frac{1}{2d} x^2 \]
が得られる。一方、極座標表示では角度を \(y\)-軸の負の方向から測ると考えると
\[ r = d-r \cos \theta \]
つまり (9-5) 式で \(e=1 \)と置いたものになる。
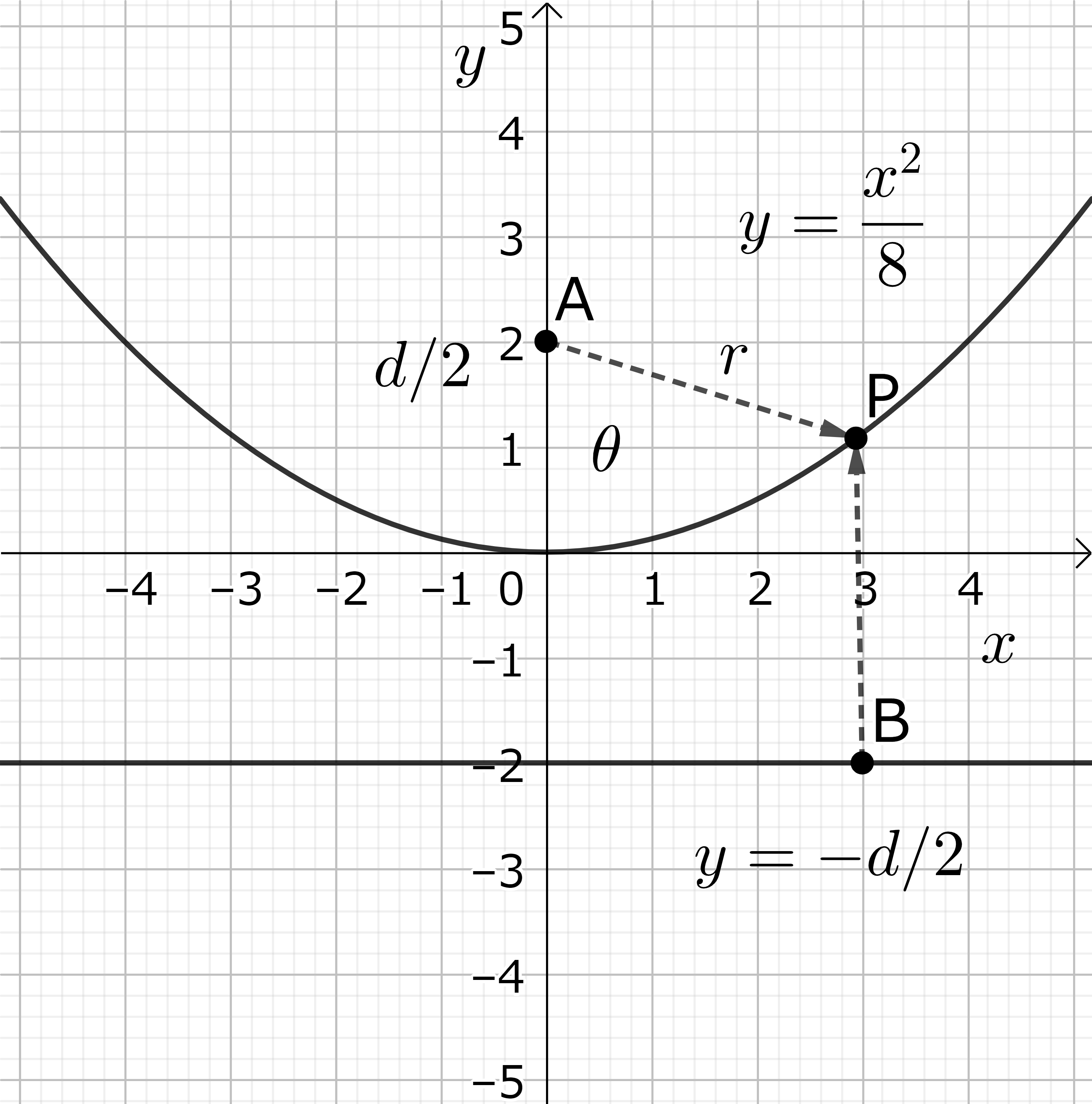
図14-1: 放物線の特徴付け
AP=BP ここに \(y=\frac{x^2}{8}\)
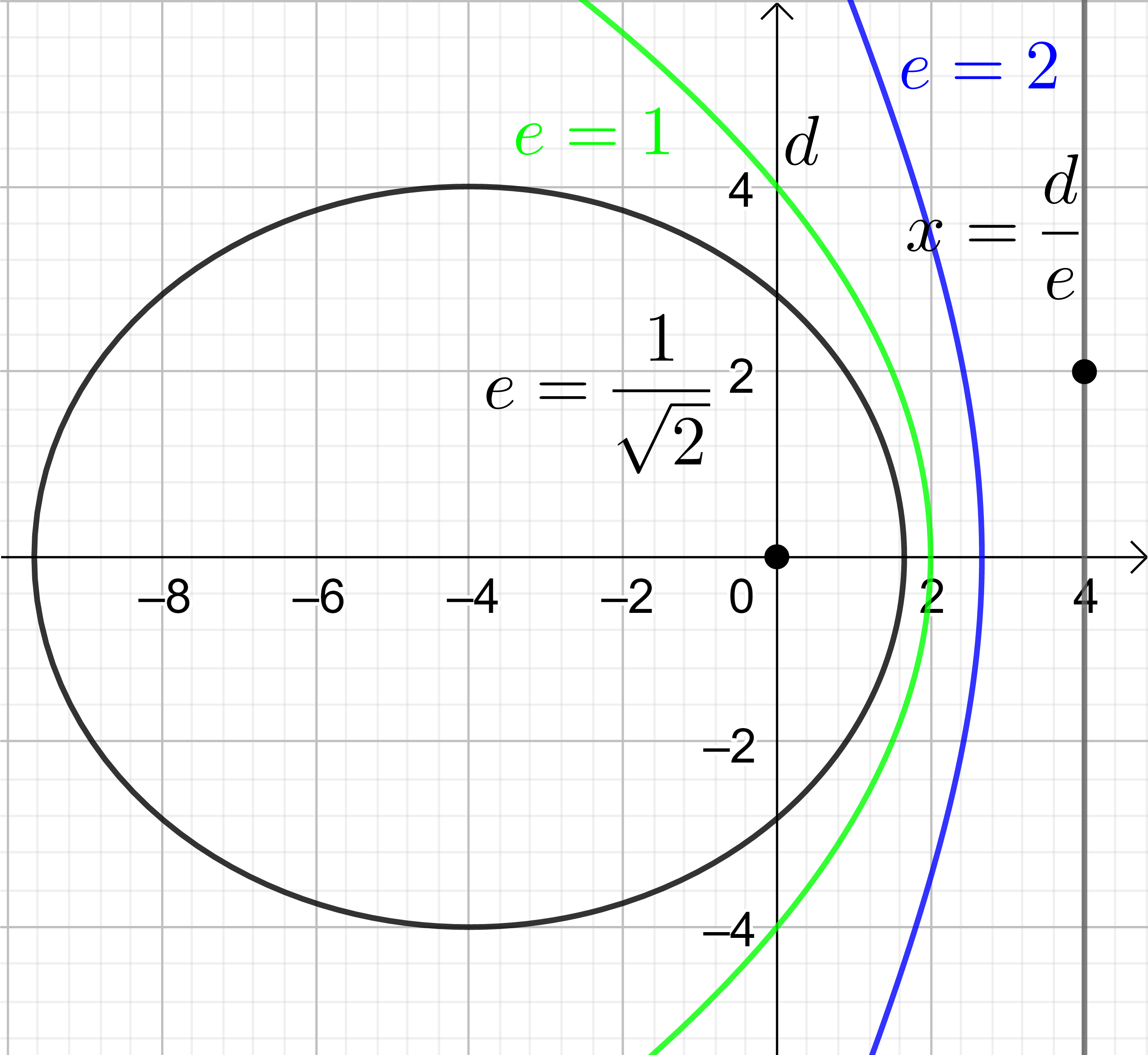
図14-2: 極座標表示の二次曲線
双曲線の直交座標での方程式は
\[ \left( \frac{x}{a}\right)^2-\left( \frac{y}{b}\right)^2=1 \tag{9-9} \]
である。この場合には \(e > 1 \)であるから楕円の場合の \(a, b, d \) の関係式は使えない。長径、短径の関係式に代わるものとして今度は \( x, y → \pm \infty \) とした場合の漸近式を取ることが出来る。\( |x|, |y| → \infty \) とすると(9-9) の左辺は非常に大きく右辺の 1 は無視できるので、\(1 → 0\) と置いて
\[ \left( \frac{x}{a}\right)^2-\left( \frac{y}{b}\right)^2=0 \tag{9-10} \]
が漸近線の方程式である。和差の積の公式により因数分解すると、この式は
\[ \frac{x}{a} \pm \frac{y}{b}=0 \tag{9-11} \]
という二つの直線の式と同等である。
-
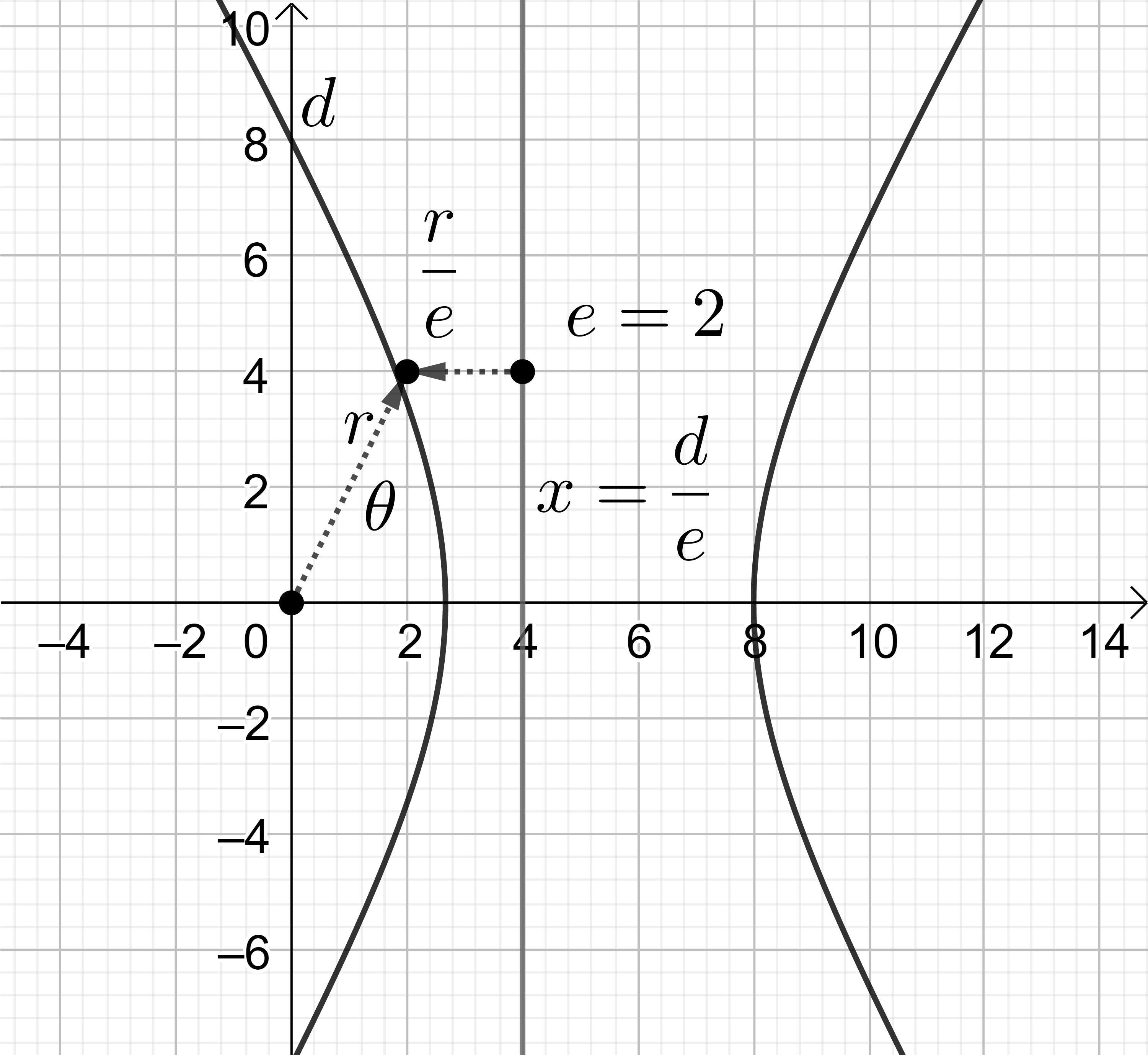
図15-1: 極座標表示の双曲線とその特徴付け (\(e > 1\))
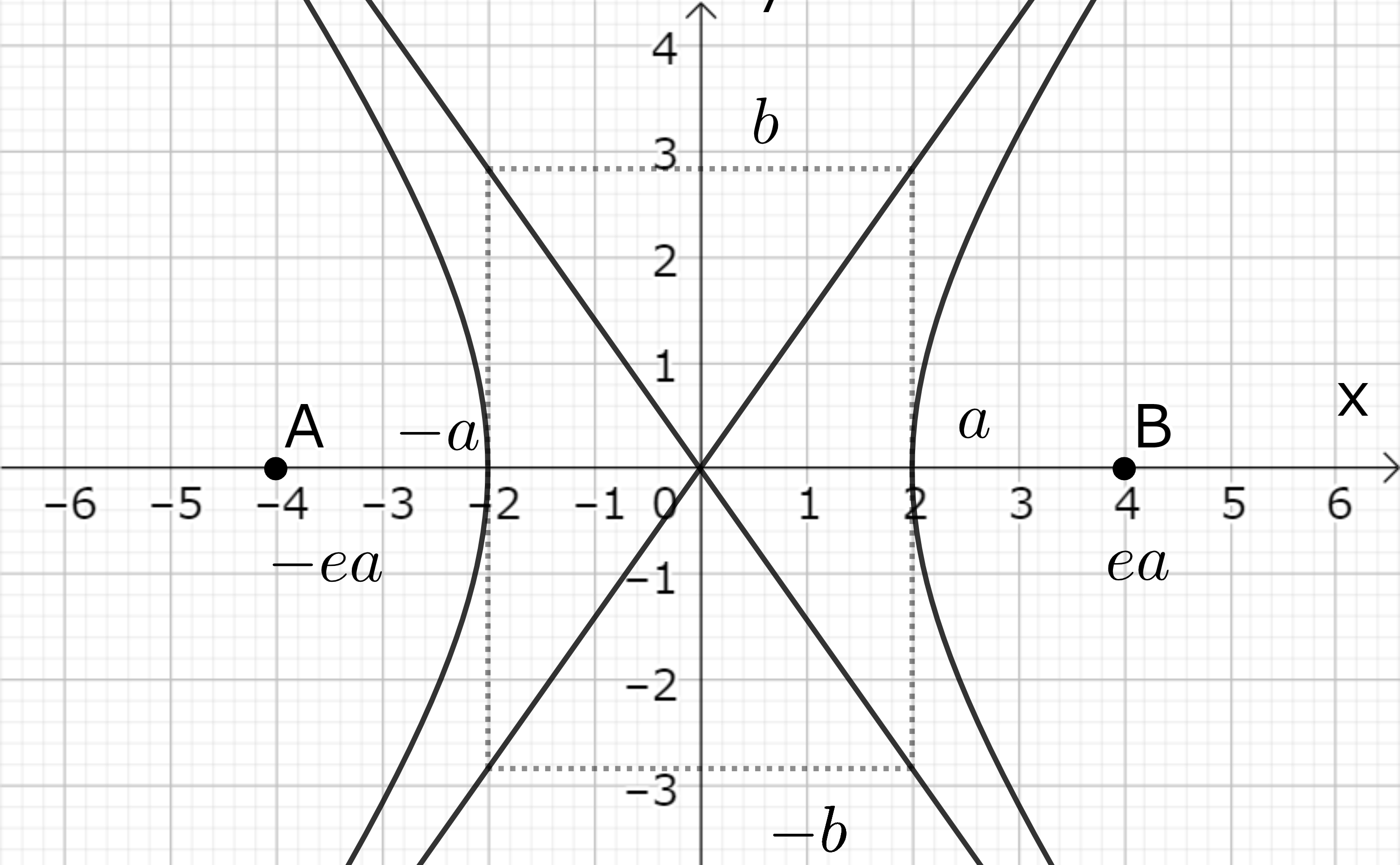
図15-2: 双曲線の漸近線、\(a=2, b=2\sqrt{3}, e=2\) の場合
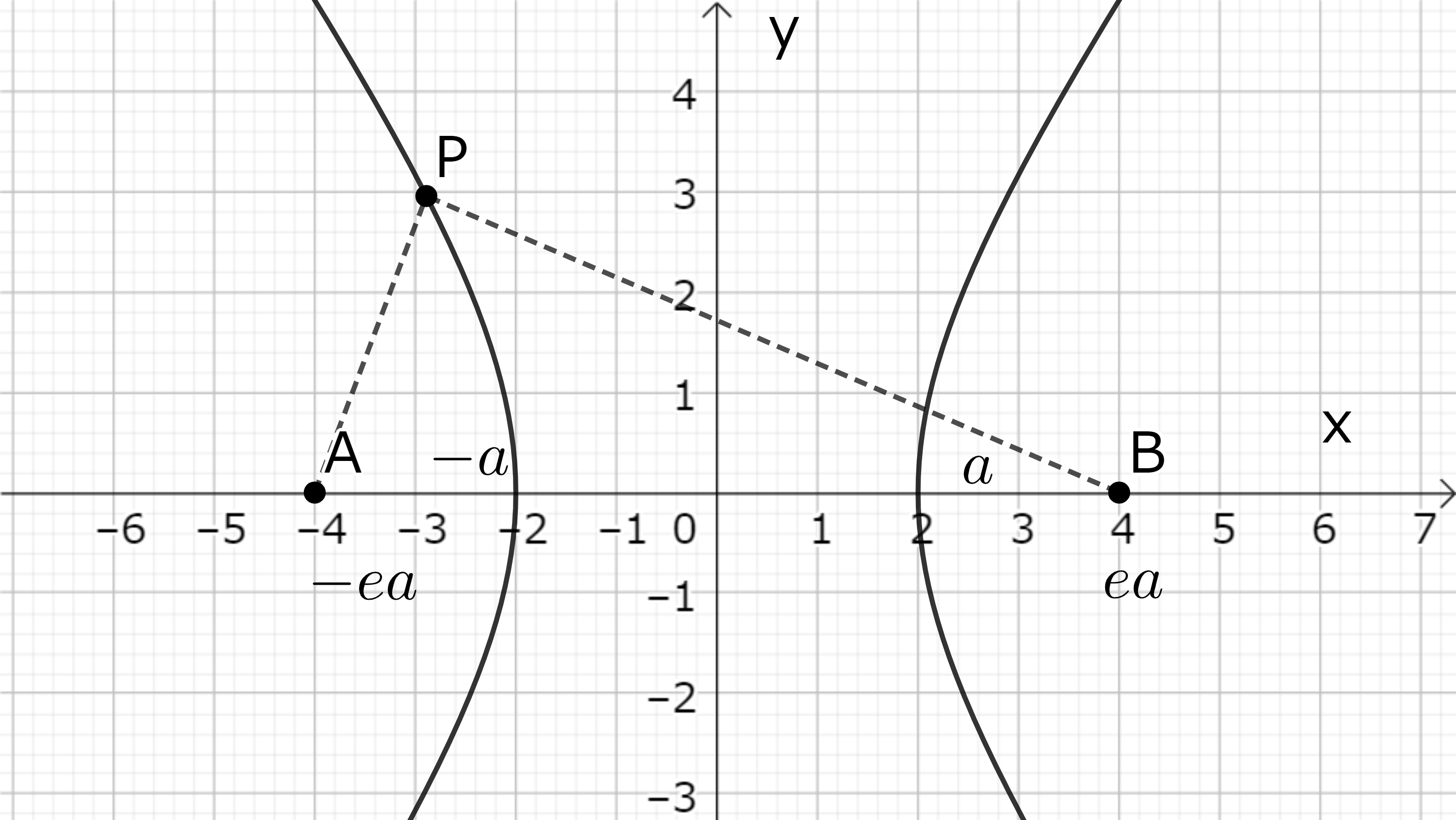
図15-3: 直交表示の双曲線とその特徴付け
双曲線の特徴は二つの焦点からの距離の差が (楕円の時の和と違って) \(2a\) と一定になる事である。二つの焦点の位置を楕円の時と同じく \( \pm ea \) と取ると、この条件は
\[ \sqrt{(x+ea)^2+y^2}-\sqrt{(x-ea)^2+y^2}=\pm 2a \]
と表わされる。左辺二項目を右辺に移項して2乗を取ると
\[ (x+ea)^2+y^2=(x-ea)^2+y^2+4a^2 \pm 4a \sqrt{(x-ea)^2+y^2} ,\\ 4eax-4a^2=\pm 4a \sqrt{(x-a)^2+y^2} ,\\ \sqrt{(x-ea)^2+y^2}=\pm (ex-a) \]
更に2乗を取ると
\[ x^2-2eax+e^2 a^2 + y^2 = e^2 x^2-2eax+a^2 ,\\ (1-e^2)x^2+y^2 = (1-e^2)a^2 \]
そこで \( (1-e^2)a^2 < 0 \) で割ると \( b=a\sqrt{e^2-1} \) として (9-9) が得られる。
双曲線の極座標表示は再び (9-5) であるが離心率 \(e\) は \( e > 1 \) である。 双曲線では \( d \) が \( d=a(e^2-1) \) である事を示すために、今度は (9-5) から直交表示の方程式を導いてみる。(9-5) を \( r=d-er\cos\ \theta \) と書き、\( x=r\cos\ \theta, y=r\sin\ \theta \) により \(x-y \)表示に移ると、\( \sqrt{x^2+y^2}=d-ex \) より2乗して
\[ x^2+y^2=(d-ex)^2=d^2-2edx+e^2 x^2 \]
まず \(e=0 \)の時はこの式は半径 \( d\) の円を表わす。次に \( e <1 \) の時は \( (1-e^2)x^2+2edx+y^2=d^2 \) を \( (1-e^2) \) で割って
\[ x^2+2\frac{ed}{1-e^2}x+\frac{y^2}{1-e^2}=\frac{d^2}{1-e^2} ,\\ \left(x+\frac{ed}{1-e^2}\right)^2+\frac{y^2}{1-e^2}=\frac{e^2 d^2}{(1-e^2)^2}+\frac{d^2}{1-e^2}=\frac{d^2}{(1-e^2)^2} ,\\ \left( \frac{x+\frac{ed}{1-e^2}}{\frac{d}{1-e^2}}\right)^2+\left( \frac{y}{\frac{d}{\sqrt{1-e^2}}} \right)^2=1 \]
そこで楕円の時の \( d=b\sqrt{1-e^2}=a(1-e^2) \) を使うと
\[ \left( \frac{x+ea}{a}\right)^2+\left( \frac{y}{b}\right)^2=1 \]
が得られる。この式は、\( x=-ea \) に中心をもつ楕円を表わす。 更に、\(e=1 \) の時は \( y^2=d^2-2dx \) は \( x=\frac{d}{2}-\frac{1}{2d} y^2 \) であり、\( x=0 \) の時 \( y=d \) で垂線を下ろすべき直線は \( x=d \) である。グラフは \(x\)-軸の負の方向に開いた放物線である。最後に \( e > 1 \) の時は
\[ (e^2-1)x^2-2edx-y^2=-d^2 ,\\ x^2-2\frac{ed}{e^2-1}x-\frac{y^2}{e^2-1}=-\frac{d^2}{e^2-1} ,\\ \left( x-\frac{ed}{e^2-1}\right)^2-\frac{y^2}{e^2-1}=\frac{e^2 d^2}{(e^2-1)^2} -\frac{d^2}{e^2-1}=\frac{d^2}{(e^2-1)^2} ,\\ \left( \frac{x-\frac{ed}{e^2-1}}{\frac{d}{e^2-1}}\right)^2-\left( \frac{y}{\frac{d}{\sqrt{e^2-1}}} \right)^2=1 \]
そこで今度は \( d=b\sqrt{e^2-1}=a(e^2-1) \) を仮定すると
\[ \left( \frac{x-ea}{a}\right)^2-\left( \frac{y}{b}\right)^2=1 \]
が得られる。この式は、\( x=ea \) に中心をもつ双曲線を表わす。
(追補-6) 物理学では二次曲線は \( \frac{1}{r^2} \) の中心力による粒子の運動として重要である。万有引力による惑星の軌道が正確な円ではなく楕円である事は、ティコ・ブラーエが蓄積した詳しい観測結果の分析を通じてケプラーによりはじめて発見された。
複素平面、オイラーの公式、ド-モアブルの定理、1 の分解
二次元直交座標で \(y\)-軸を複素数 \( z=x+yi \) の虚数部分と考えて虚軸 \( yi \) としたものを複素平面という。(図16-1 参照) この時 \(x\)-軸を実軸という。実軸の単位は 1、虚軸の単位は \( i \) である。これにより、複素数は複素平面上の点として一意的に表わされる。極座標表示では、\( x=r \cos \theta, y=r \sin \theta \) より、 \( z=r(\cos \theta +i \sin \theta) \) である。解析分野のところで詳しく学ぶが、数の概念を複素数まで拡張すると、三角関数は指数関数と実は同じものであり、ラジアンで測った実数の一般角 \( \theta\) に対して
\[ e^{i\theta}=\cos \theta + i \sin \theta \tag{10-1} \]
が成り立つ。ここに \( e=2.7182 ...\) は「数について」のところで出て来たネピア数 (自然対数の底) である。(1) をオイラーの公式 (Euler’s formula) という。(Leonhard Euler は18世紀の数学者) これを使うと複素数 \( z \) は
\[ z=r e^{i \theta} \tag{10-2} \]
と書ける。これを複素数の極座標表示といい、\( r=|z| ≧ 0 \) を複素数の絶対値、\( -\infty < \theta < \infty \) を偏角という。(10-2) の (自然) 対数を取ると
\[ \log z=\log r+i \theta \tag{10-3} \]
偏角を \( 0 ≦ \theta < 2\pi \) あるいは \( -\pi ≦ \theta < \pi \) に制限する場合には
\[ \log z=\log r+i (\theta+2\pi n) \quad n \in \boldsymbol{Z} \tag{10-4} \]
と書いて、ある特定の \( n\) をもつ (10-4) 式を \( \log z \) の分岐 (branch) という。(10-1) で \( \theta=2\pi \) とおくと \( \cos 2\pi=1, \sin 2\pi=0 \) より \( e^{2\pi i}=1 \) である。また、任意の整数 \( n\) に対して
\[ e^{2\pi n i}=1\ , \quad \cos 2\pi n=1\ , \quad \sin 2\pi n=0 \quad \hbox{for}\ n\in \boldsymbol{Z} \tag{10-5} \] が成り立つ。更に
\[ e^{i (\theta+2\pi n)}=e^{i \theta} , \\ \cos (\theta+2\pi n)=\cos \theta , \\ \sin (\theta+2\pi n)=\sin \theta \quad \hbox{for}\ n\in \boldsymbol{Z} \tag{10-6} \]
一般に
\[ f(x+2\pi)=f(x) \quad \hbox{}^\forall x \in \boldsymbol{R} \tag{10-7} \]
を満たす関数 \( f(x) \) を周期 \( 2\pi \) をもつ周期関数という。\( e^{i \theta}, \cos \theta, \sin \theta \) は、いずれも周期 \( 2\pi \) をもつ周期関数である。また、複素指数関数 \( e^z \) は、周期 \( 2\pi i \) をもつ周期関数である。 \[ e^{(z+2\pi i)}=e^z \tag{10-8} \]
複素数まで拡張した場合の指数法則 \( (e^z)^n=e^{nz} \) を用いると、任意の整数 \( n \in \boldsymbol{Z} \) に対して
\[ (\cos \theta + i \sin \theta )^n=(e^{i \theta})^n=e^{i n \theta} \\ =\cos (n\theta) + i \sin (n\theta) \tag{10-9} \]
これをド-モアブルの定理 (de Moivre’s theorem) という。また、任意の角度 \( \alpha, \beta \) に対して
\[ (\cos \alpha + i \sin \alpha) (\cos \beta + i \sin \beta) \\ =\cos (\alpha+\beta) + i \sin (\alpha+\beta) \tag{10-10} \]
が指数法則 \( e^{i \alpha} e^{i \beta}=e^{i (\alpha+\beta)} \) を考える事によって容易に導ける。ここから、両辺の実部と虚部を比較することによって三角関数の加法定理
\[ \cos (\alpha+\beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta , \\ \sin (\alpha+\beta)=\sin \alpha \cos \beta + \cos \alpha \sin \beta \tag{10-11} \]
を導く事が出来る。
(練習問題) 三角関数の加法定理 (10-11) を導け。
\(n\) 次方程式 \( z^n-1=0 \quad n \in \boldsymbol{N} \) の解は
\[ \omega=e^{\frac{2\pi}{n} i}=\cos \frac{2\pi}{n}+i \sin \frac{2\pi}{n} \tag{10-12} \]
として、\( \omega^m\) (\(m=0, 1, 2, \cdots, n-1\)) で与えられる。これは
\[ (\omega^m)^n=\omega^{nm}=\left( e^{\frac{2\pi i}{n}} \right)^{nm}=e^{2m\pi i} =\cos 2m\pi + i\sin 2m\pi = 1 \]
であるからである。これらは、複素平面における半径 1 の円 \( |z|=1 \) (これを単位円という) の上に等間隔に分布している。(図16-2 参照) 例えば、 \( n=3 \) の時は以前見た様に 1 と
\[ e^{\frac{2\pi}{3} i}=\cos \frac{2\pi}{3}+i\sin \frac{2\pi}{3} =\frac{-1+\sqrt{3} i}{2}=\omega \quad , \\ e^{\frac{4\pi}{3} i}=\cos \frac{4\pi}{3}+i\sin \frac{4\pi}{3}=\frac{-1-\sqrt{3} i}{2}=\omega^2 = \omega* \]
である。これを 1 の分解という。
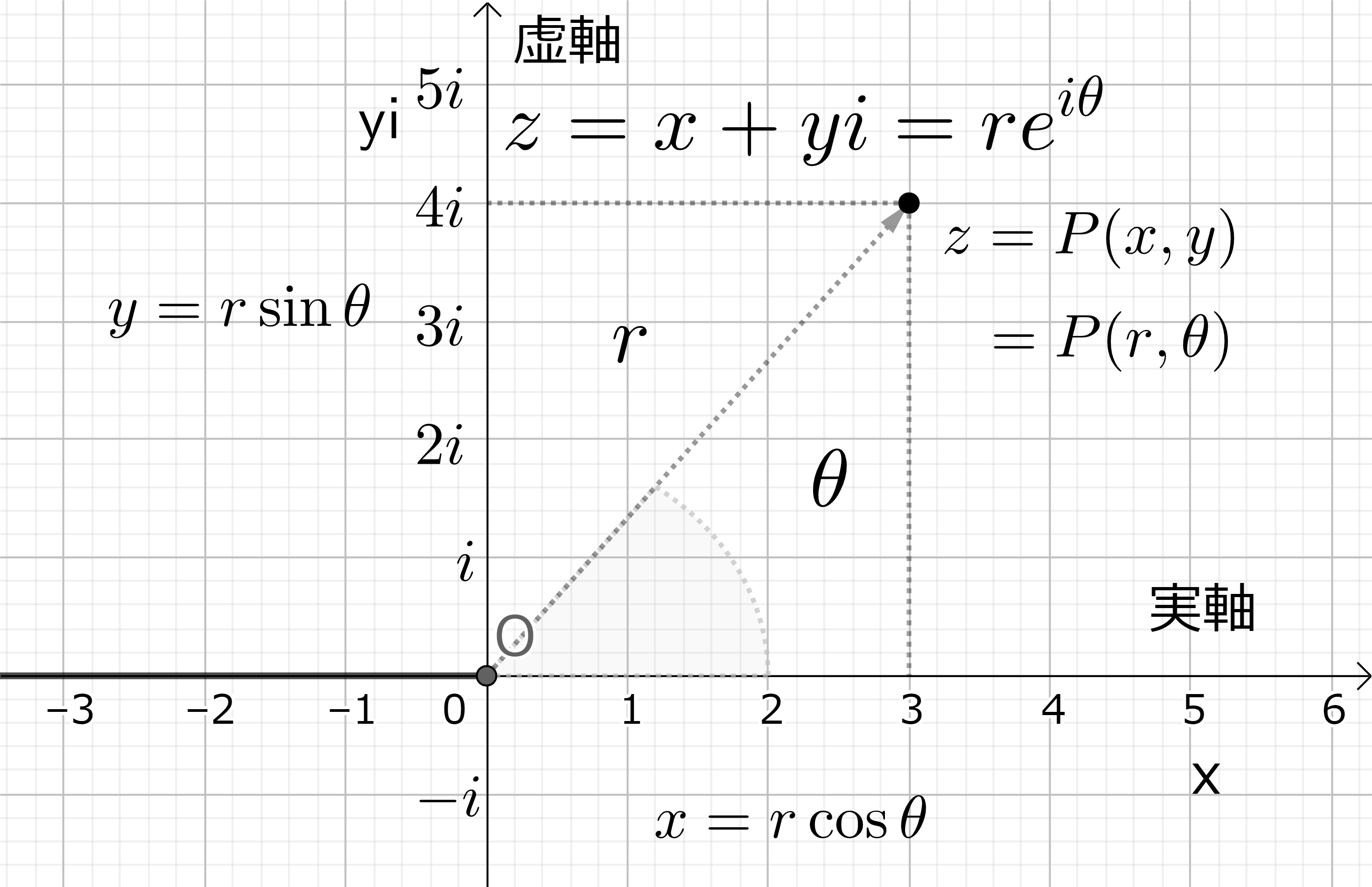
図16-1: 複素平面
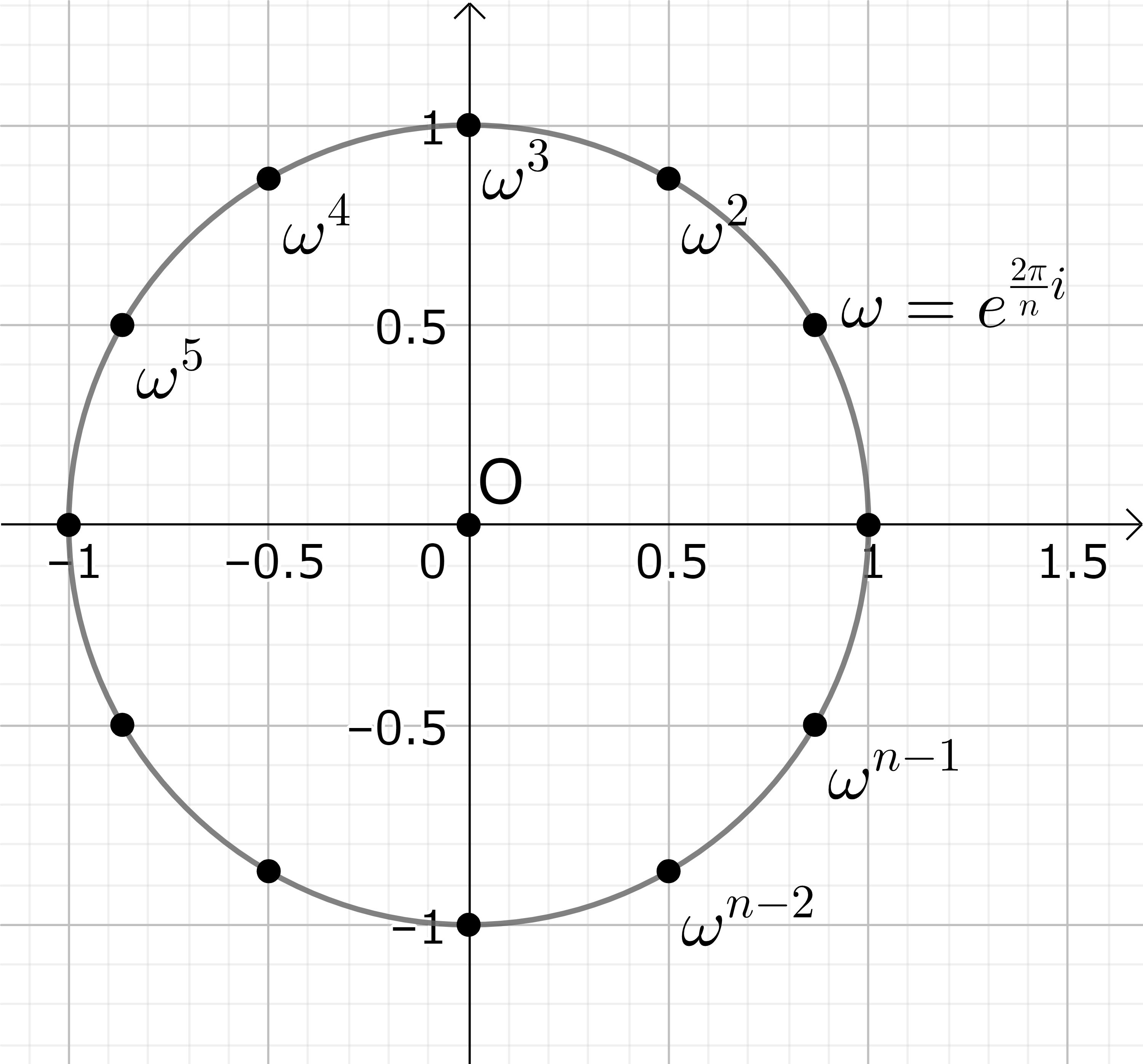
図16-2: 1 の分解
.
三次方&程式の根の公式 : カルダノの式
一般の三次方程式 \( ax^3+bx^2+cx+d=0 \quad (a \neq 0) \) に対しては、二次方程式の様な根の公式を求める事が出来る。ここに、係数 \( a, b, c, d \) は有理数、または整数と仮定する。まず全体を \( a\) で割っておいて、新しく係数を定義し直して \( x^3+ax^2+bx+c=0 \) としておく。次に \( x=X-\frac{a}{3} \) と変数変換して \( X \) の方程式に移ると、 \( X^2 \) の項は常に消去することができる。そこで \( X\) を再び \( x\) と書いて、もう一度係数を定義し直すと、一番一般的な三次方程式として
\[ x^3+ax+b=0 \tag{11-1} \]
だけを考えれば良い事が分かる。
三次関数のところで既に述べた様に、(11-1) の解のおよその様子は三次関数 \( f(x)=x^3+ax+b \) のグラフを描くことによって容易に知ることが出来る。(図17, 18 参照) まずこのグラフは \( y=x^3 \) と \( y=ax+b \) とを組み合わせて得られる事に注意すると、最も簡単な場合は \(a=b=0 \) で \( y=x^3 \) は \( x\)-軸と \( x=0 \) だけで交わり、\( x^3=0 \) は \( x=0 \) に 3 重根を持つ。次に、\( y=ax+b \) の直線のグラフに \( y=x^3 \) のグラフを積み上げると、\( a > 0 \) の時は簡単に \( y=x^3+ax+b \) は \( x\)-軸と或る一点だけで交わり、従ってこれは 1 つの実根と互いに複素共役な二つの複素数解を持つ場合であることが分かる。(図17-2) 問題は \( a < 0 \) の場合で、特に更に \( b=0\) の場合を考えると \( y=x^3+ax=x^3-|a|x \) は図18-1 の様なグラフで、方程式 \( x^3+ax=0 \)、つまり \( x(x^2-|a|)=0 \) は \( x=0\) と \( x=\pm \sqrt{|a|} \) の3つの実根を持っている事が分かる。後で解析分野で学ぶ 微分法を使うと、関数 \( y=x^3+ax \ (a < 0) \) の極大、極小値 (そこで関数の値が局所的に最大、最小になっている点) は \( 3x^2-|a|=0 \) から求められる。すなわち、\( x= \pm \sqrt{\frac{|a|}{3}} \) を \( y= x^3-|a|x \) に代入して、\( y=\mp \frac{2|a|}{3} \sqrt{\frac{|a|}{3}}=\mp 2 \left(\sqrt{\frac{|a|}{3}}\right)^3 =\mp 2 \sqrt{\left(\frac{|a|}{3}\right)^3} \) が関数 \( y=x^3+ax \ (a < 0) \) の極小、極大値 である。\( b \neq 0 \) の場合は、このグラフを \( y\)-軸の正の方向に \( b\) だけずらして図18-2 の様になる。この場合の三次方程式 \( x^3+ax+b=0 \ (a < 0) \) の解の様子は、極小、極大点と \( x\)-軸との互いの位置関係に依存する。すなわち
\[ 1. \ b-2\sqrt{\left(\frac{|a|}{3}\right)^3} < 0 < b+2\sqrt{\left(\frac{|a|}{3}\right)^3} \ の時、\\ \quad \quad 3つの異なる実根 \\ 2. \ b+2\sqrt{\left(\frac{|a|}{3}\right)^3} < 0 \ の時、\\ \quad \quad 一つの正の実根と互いに複素共役な二つの複素数解 \\ 3. \ b-2\sqrt{\left(\frac{|a|}{3}\right)^3} > 0 \ の時、\\ \quad \quad 一つの負の実根と互いに複素共役な二つの複素数解 \tag{11-2} \]
ここに、1, 2, 3 の条件は
\[ D=\left(\frac{b}{2}\right)^2-\left(\frac{|a|}{3}\right)^3 \tag{11-3} \]
として、それぞれ \( D < 0, D > 0, D > 0 \) と書くことができる。(証明せよ。)
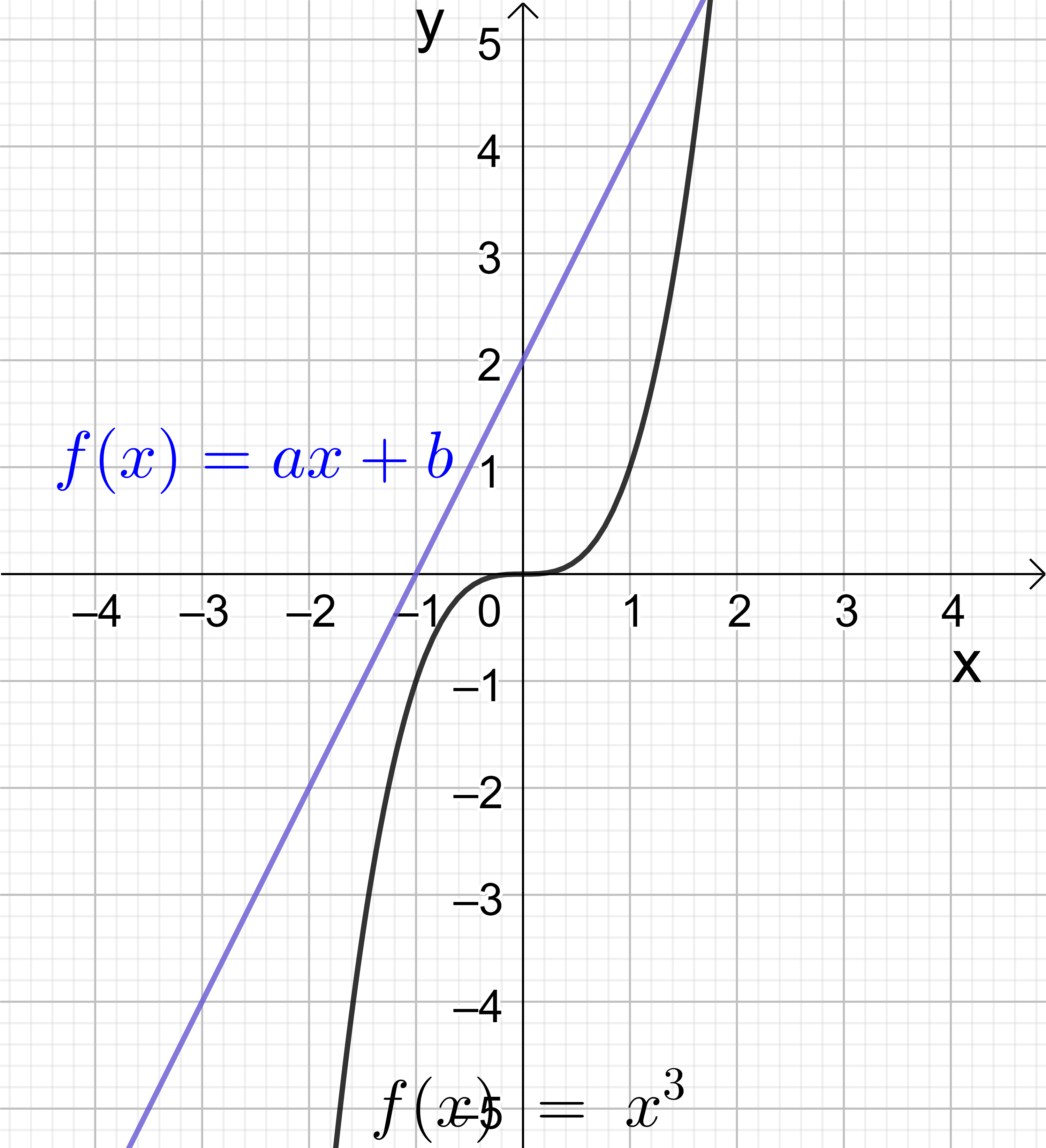
図17-1: \(y=x^3\) と \(y=ax+b\) のグラフ、 \(a=2, b=2\) の場合
図17-2: \(y=x^3+ax+b\) \((a > 0)\) のグラフ、\(a=2, b=2\)
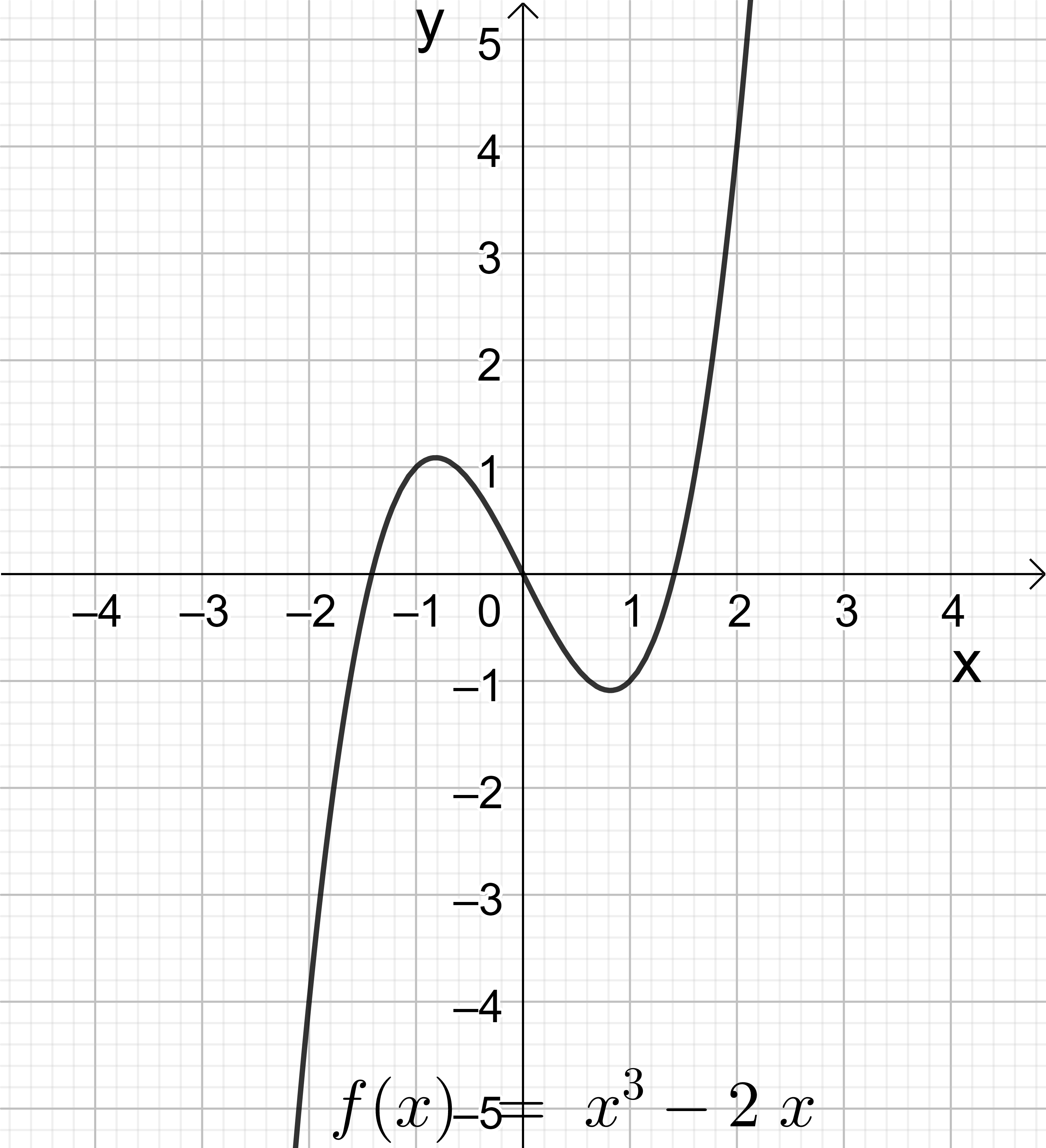
図18-1: \(y=x^3+ax\) \((a < 0)\) のグラフ、 \(a=-2\) の場合
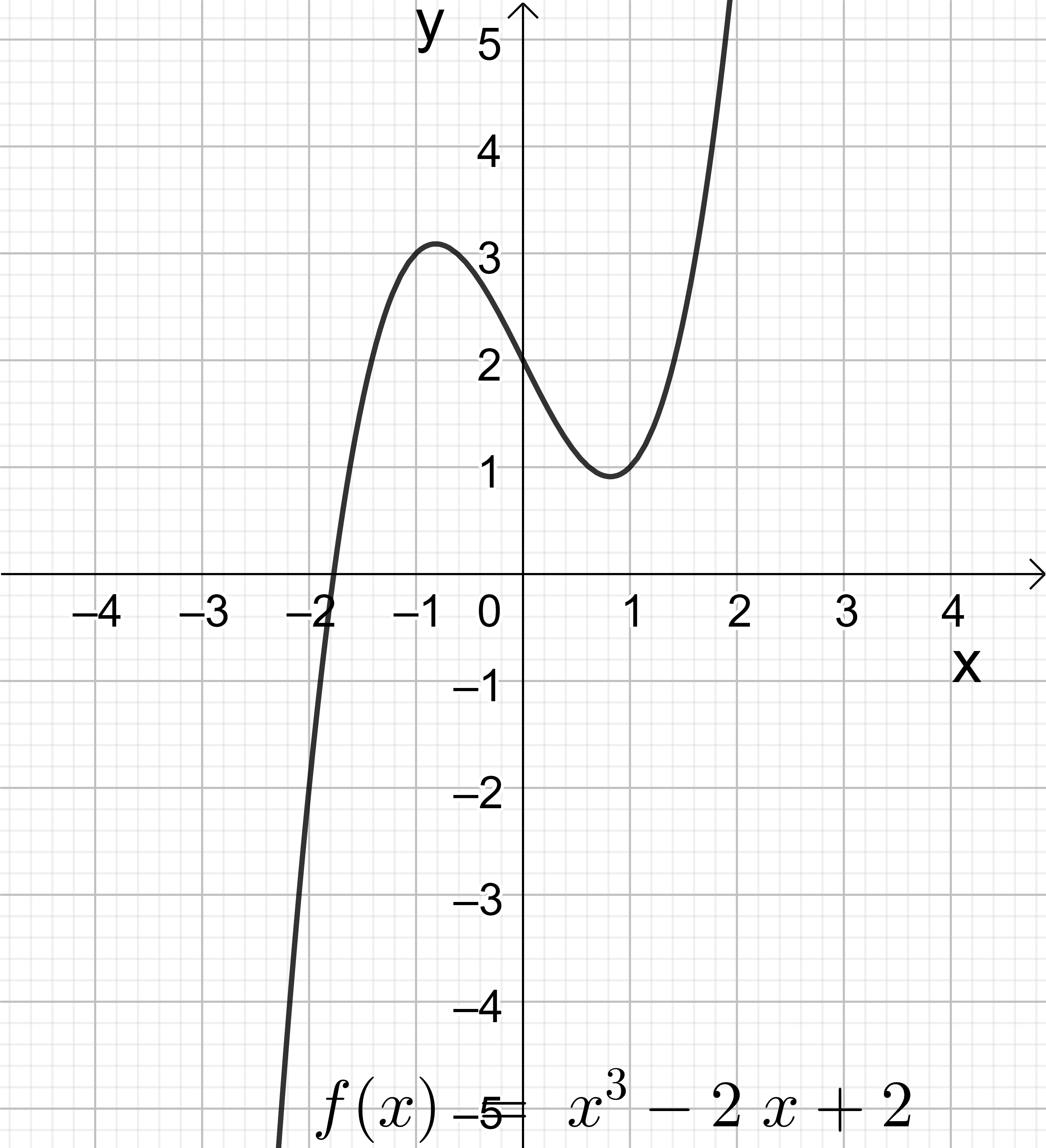
図18-2: \(y=x^3+ax+b\) のグラフ、\(a=-2, b=2\) の場合
.
一般に任意の \( a\) に対して
\[ D=\left(\frac{b}{2}\right)^2+\left(\frac{a}{3}\right)^3 \tag{11-4} \]
を三次方程式の判別式という。(11-3) は \( a< 0 \) の特別の場合である。\( a > 0\) の場合は勿論 \( D > 0\) であるので、三次方程式 (11-1) の解の性質として次の簡単な規則が成り立つ。
\[ 1.\ D < 0 \ の時、3つの異なる実根 \\ 2.\ D = 0 \ の時、1つの実根と2つの重根 \\ 3. \ D > 0 \ の時、1つの実根と互いに複素共役な \\ \quad \qquad 2つの複素数解 \tag{11-5}\]
(注意) 2つの複素数解がある時それらが互いに複素共役である事は、今考えている三次方程式が実数係数の三次方程式である事から明らかである。
(11-1) 式の方程式を解くために公式
\[ (x+y+z)(x^2+y^2+z^2-xy-yz-zx) \\ =(x+y+z)(x+\omega y+\omega^2 z)(x+\omega^2 y+\omega z) \\ =x^3+y^3+z^3-3xyz \tag{11-6} \]
を利用する。ここに、\( \omega=\frac{-1+\sqrt{3} i}{2}=e^{\frac{2\pi}{3} i} \) である。そこで
\[ 3yz=-a \quad , \quad y^3+z^3=b \tag{11-7} \]
として、ここから \( y, z\) が求まったとすると 、(11-1) の解は
\[ x =-y-z \quad , \quad -\omega y-\omega^2 z \quad , \quad -\omega^2 y-\omega z \tag{11-8} \]
と求まることになる。
(11-7) を解くには、\( y^3+z^3=b, y^3 z^3=-\left(\frac{a}{3}\right)^3 \) より、二次方程式の根と係数の関係から \( y^3\) と \( z^3\) は次の二次方程式を解く事によって得られる。
\[ t^2-bt-\left(\frac{a}{3}\right)^3=0 \tag{11-9} \]
そこで
\[ y^3 , z^3 =\frac{b}{2} \pm \sqrt{\left( \frac{b}{2}\right)^2+\left(\frac{a}{3}\right)^3} =\frac{b}{2} \pm \sqrt{D} \tag{11-10} \]
ここに \( D\) は (11-4) で定義した三次方程式 (11-1) の判別式である もし \( D > 0 \) なら
\[ y=\sqrt[3]{\frac{b}{2} + \sqrt{D} } \quad , \quad z=\sqrt[3]{\frac{b}{2} - \sqrt{D}} \tag{11-11} \]
は実数であるから、(11-8) は一つの実数解と二つの互いに複素共役な複素数解を与える。\( D = 0 \) の時は、\( y=z=\sqrt[3]{\frac{b}{2}} \) であり、\( \omega+\omega^2=-1 \) より、1つの実根 \( -2y\) と2つの重根 \( y\) となる。この場合、\( b \neq 0 \) である限り \( a < 0\) であり、\( \left(\frac{b}{2} \right)^2=\left(\frac{|a|}{3}\right)^3 \) つまり、\( b > 0\) なら \( y=z=\sqrt{\frac{|a|}{3}} \) から1つの実根は \( -2\sqrt{\frac{|a|}{3}} \)、2つの重根は \( \sqrt{\frac {|a|}{3}} \) である。これは、(11-2) の 3. の \( D → 0\) の極限の場合である。もし \( b < 0\) なら (11-2) の 2. の極限の場合になる。
問題は \( D < 0\) の場合である。この場合は、必ず \( a < 0\) となる。(11-10) から \( y^3, z^3\) は互いに複素共役な複素数となるが、複素数の三重根を正しく計算すると、(11-8) は全て実数になることが分かる。複素数の \( n\) 乗根については、次の (追補-7)で詳しく述べるが、ここでは、\( y, z\) を極座標表示する事を考える。 \( D < 0\) の時 (11-10) を \( \frac{b}{2} \pm i \sqrt{|D|} \) と書くと、この複素数の絶対値の2乗は
\[ \left( \frac{b}{2}\right)^2+|D| \\ = \left( \frac{b}{2}\right)^2 -\left( \frac{b}{2}\right)^2-\left(\frac{a}{3}\right)^3 =-\left(\frac{a}{3}\right)^3=\left(\frac{|a|}{3}\right)^3 > 0 \]
そこで
\[ \frac{b}{2} \pm i \sqrt{|D|}=R e^{\pm i \theta} \tag{11-12} \]
と書くと
\[ R=\left( \sqrt{\frac{|a|}{3}}\right)^3 \quad , \quad \cos \theta = \frac{\frac{b}{2}}{R} \]
ここに、\( D < 0\) より \( -1 ≦ \cos\ \theta ≦ 1 \) だから \( 0 ≦ \theta ≦ \pi \) が一意的に決まる。そこで、\( r=\sqrt{\frac{|a|}{3}} \) と置いて \( R=r^3\) を使うと
\[ y, z=r e^{\pm i \frac{\theta}{3}} \]
となる。そこで (11-8) は
\[ x =-y-z =-r \left( e^{i \frac{\theta}{3}}+e^{-i \frac{\theta}{3}} \right) =-2 r \cos \frac{\theta}{3}, \\ x=-\omega y-\omega^2 z =-r \left( e^{i \frac{2\pi}{3}} e^{i \frac{\theta}{3}}+e^{-i \frac{2\pi}{3}} e^{-i \frac{\theta}{3}} \right) \\ =-r \left( e^{i \frac{\theta+2\pi}{3}}+e^{-i \frac{\theta+2\pi}{3}} \right)5 =-2 r \cos \frac{\theta+2\pi}{3} ,\\ x=-\omega^2 y-\omega z =-r \left( e^{i \frac{-2\pi}{3}} e^{i \frac{\theta}{3}}+e^{i \frac{2\pi}{3}} e^{-i \frac{\theta}{3}} \right) \\ =-r \left( e^{i \frac{\theta-2\pi}{3}}+e^{-i \frac{\theta-2\pi}{3}} \right) =-2 r \cos \frac{\theta-2\pi}{3} \tag{11-13} \]
と3実根となる。ここに、\( r\) と \( \theta \) は
\[ r=\sqrt{\frac{|a|}{3}} \quad , \quad \cos \theta = \frac{\frac{b}{2}}{r^3} \quad ( 0 ≦ \theta ≦ \pi ) \tag{11-14} \]
である。これが (11-5) の 1. の場合である。
(追補-7) 複素数の \( n\) 乗根について: 一般に \( a \in \boldsymbol{R} \) を任意の実数とする時、複素数 \( z\) の \( a\) べき乗は複素数の対数関数 (自然対数) \( \log z\) を使って
\[ z^a=e^{a \log z} \tag{11-15} \]
として定義される。特に、\( z\) の極座標表示 (10-2) を使うと (10-4) より
\[ \left( r e^{i \theta} \right)^a =e^{a \left(\log r+i (\theta+2\pi n)\right)} =r^a e^{i a(\theta+2\pi n)} \]
当選のことながら、この様な定義は対数関数の branch の取り方 \( n\) の値に依存する。 一番簡単には対数関数の cut の位置を実軸の負の方向に取り
\[ -\pi < \theta ≦ \pi \ ,\quad n=0 \tag{11-16} \]
とする。この時、\( z\) の三乗根は \( a=\frac{1}{3} \) として
\[ \sqrt[3]{z}=z^{\frac{1}{3}}=\sqrt[3]{|z|} e^{i \frac{\theta}{3}} \]
となる。ここに \( \theta \) は (11-16) の branch で取った \( z\) の偏角である。
四次方程式の解法、フェラーリの式、更に高次の代数方程式について
有理数係数 (或いは整数係数) をもつ四次方程式
\[ ax^4+bx^3+cx^2+dx+e=0 \quad (a \neq 0) \tag{12-1} \]
に対しても、二次方程式と三次方程式の場合と同様に一般的な解公式を書き下すことができる。ここでは、\( x^2\) と \( x\) の完成平方式を使ったフェラーリの方法について概説する。まず三次方程式の場合と同様に全体を \( a\) で割っておき、\( x\) の平行移動により \( x^3\) の係数を消去する。そこで、一番一般的な四次方程式として
\[ x^4+ax^2+bx+c=0 \tag{12-2} \]
を考えれば充分である。ここでもし \( b=0\) なら、(12-2) は \( x^2\) の二次方程式で二次方程式の根の公式により、それらが2実数解であれ互いに複素共役な複素数解であれ、いずれもそれらの \( \pm \)平方根を取る事により複素数の範囲内で4つの解を全て求める事が出来る。従って、以下では常に \( b \neq 0 \) を仮定する事にする。
まず或る実数 \( r\) を考えて
\[ \left(x^2+\frac{r}{2}\right)^2-\left[(r-a)x^2-bx+\left( \frac{r}{2}\right)^2-c\right]=0 \tag{12-3} \]
ここに、左辺の \( \left[ ... \right] \) の部分が \( x\) の一次式の完成平方式になる様に \( r\) を決定する。そのためには、この部分の \(x\) の二次式の判別式が 0 となる様にすれば良い。すなわち
\[ b^2+4(r-a)\left[ c-\left(\frac{r}{2}\right)^2\right]=0 , \\ b^2-(r-a)(r^2-4c)=0 , \\ r^3-ar^2-4cr+(4ac-b^2)=0 \tag{12-4} \]
三次方程式のところで詳しく述べた様に、(12-4) は必ず最低1個は実数解を持つ。そこでこの実数 \( r\) を一つ固定すると、(12-3) の \( \left[ ... \right] \) 部分は
\[ \left( \sqrt{r-a} x-\frac{b}{2\sqrt{r-a}}\right)^2-\frac{b^2}{4(r-a)}+\frac{r^2}{4}-c \\ =\left( \sqrt{r-a} x-\frac{b}{2\sqrt{r-a}}\right)^2 \\ =(px-q)^2 \tag{12-5} \]
ここに1行目で完全平方以外の部分は、条件 (12-4) によって消える。 また \( p, q\) は
\[ p=\sqrt{r-a}\ , \quad q=\frac{b}{2\sqrt{r-a}} \tag{12-6} \]
である。ここに (12-4) から、\( b \neq 0 \) の時は \( r=a\) ではあり得ない。 そこで、\( r-a > 0\) or \( r-a < 0 \) である。(12-6) 式を使うと (12-3) 式は
\[ \left(x^2+\frac{r}{2}\right)^2-(px-q)^2=0 \tag{12-7} \]
と書けるので、和差の積の公式から
\[ \left( x^2+px-q+\frac{r}{2} \right) \left( x^2-px+q+\frac{r}{2} \right)=0 \tag{12-8} \]
となる。そこで \( r-a > 0 \) の時は \( p, q\) は実数で、(12-8) は実数係数の二つの二次方程式を与える。二次方程式の根の公式を使う事により、複素数の範囲内で4つの解が求まる。一方 \( r-a < 0 \) の時は \( \sqrt{r-a} \) は純虚数で、(12-6) を
\[ p=\sqrt{|r-a|}\ , \quad q=\frac{b}{2\sqrt{|r-a|}} \tag{12-9} \]
と一般化しておくと (12-7) は
\[ \left(x^2+\frac{r}{2}\right)^2+(px+q)^2=0 \tag{12-10} \]
(12-8) は
\[ \left( x^2+ipx+iq+\frac{r}{2} \right) \left( x^2-ipx-iq+\frac{r}{2} \right)=0 \tag{12-11} \]
となる。ここに \( p, q\) は (12-9) で与えられる実数である。複素係数の二次方程式はこれまで遭遇したことがないが、\( x^2 \pm ipx \pm iq+\frac{r}{2}=0 \) に単純に根の公式を適用すると
\[ x =\frac{i p}{2} \pm \sqrt{-\frac{p^2}{4}-\frac{r}{2}+iq} \quad , \\ = \frac{-i p}{2} \pm \sqrt{-\frac{p^2}{4}-\frac{r}{2}-iq} \tag{12-12} \]
が得られる。(追補-7)で見た様に、複素数の平方根は複素数の極座標表示を考える事によって一意的に決定する事ができる。
一般に有理数係数 (或いは整数係数) をもつ \( n\)次方程式
\[ a_n x^n+a_{n-1} x^{n-1}+ ... +a_1 x+a_0=0 \quad (a_n \neq 0) \tag{12-13} \]
を \( n\) 次代数方程式という。これが有限回の加減乗除と階乗根を取る操作だけで一般的に解けるかどうかは大問題であった。 \( n ≧ 5\) の場合には4次方程式までの様な根の公式を導けない事は、19 世紀の初め頃二人の若い天才数学者、ノルウェーのニールス・アーベルとフランスのエヴァリスト・ガロアによって別々に証明された。特にガロアは、現代代数学の基礎となった群論の創始者としても知られている。これらについては、高等学校数学の範囲を遥かに超えるのでここではこれ以上深入りしない事にする。
(代数分野の項、終了)
Designed by CSS.Design Sample