


: 中心力による運動
: 物理学基礎論 A
: 質点系の運動
7.1 2 質点系の運動
質点系の運動の特別な場合として、中心力の内力だけが働く 2 質点系の
運動を考えると、2 体系の運動方程式は一定速度の運動を続ける重心系
の運動と 2 質点の相対運動に対する 1 体問題に帰着される。
そこでは、2 質点の位置ベクトルの重心、相対変換が基本的である。
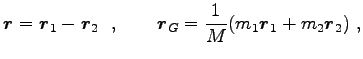 |
|
|
|
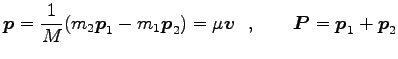 |
|
|
(0) |
ここに、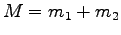 は全質量、
は全質量、
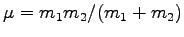 は換算質量である。
運動方程式 Eq.(6.33) は
は換算質量である。
運動方程式 Eq.(6.33) は
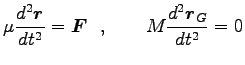 |
|
|
(0) |
となり、外力が働かないから
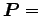 一定、となる。
角運動量保存則は
一定、となる。
角運動量保存則は
![$\displaystyle {\boldsymbol M}^\prime=[{\boldsymbol r}\times {\boldsymbol p}]=\h...
...\qquad
{\boldsymbol M}_G=[{\boldsymbol r}_G \times {\boldsymbol P}]=\hbox{一定}$](img7.png) |
|
|
(0) |
であり、相対運動は一定平面のみで起こる。
もし、内力が保存力なら、重心系でのエネルギー 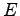 は、重心運動の
エネルギーとともに保存され
は、重心運動の
エネルギーとともに保存され
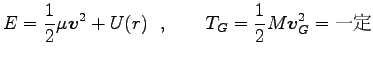 |
|
|
(0) |
となる。ここに、
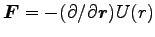 、
かつ
、
かつ
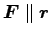 である。
である。
以下、相対運動だけに注目して、これを 2 次元の極座標表示で解く。
まず、内部角運動量は、
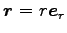 ,
,
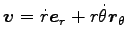 として
として
![$\displaystyle {\boldsymbol M}^\prime=\mu [{\boldsymbol r}\times {\boldsymbol p}...
...bol e}_r \times {\boldsymbol e}_\theta]
=\mu r^2 \dot{\theta} {\boldsymbol e}_z$](img14.png) |
|
|
(0) |
ここに、
![$ {\boldsymbol e}_z=[{\boldsymbol e}_r \times {\boldsymbol e}_\theta]$](img15.png) は
は 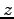 -軸方向への単位ベクトル
である。ここから
-軸方向への単位ベクトル
である。ここから
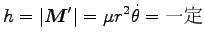 |
|
|
(0) |
中心力を
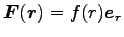 とすると、Eq. (7.2) の相対運動の
方程式は
とすると、Eq. (7.2) の相対運動の
方程式は
![$\displaystyle \mu [\ddot{r}-r(\dot{\theta})^2]=f(r)\ \ ,
\qquad
\mu (2 \dot{r} \dot{\theta}+r \ddot{\theta})=0$](img19.png) |
|
|
(0) |
と表わされる。2 番目の式は、Eq. (7.6) の角運動量保存則と同等であり、また
次の面積速度が一定という表現と同値である。
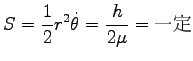 |
|
|
(0) |
Eq. (7.6) から得られる
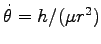 を Eq. (7.7) の
動径方向の方程式に代入すると
を Eq. (7.7) の
動径方向の方程式に代入すると
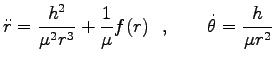 |
|
|
(0) |
ここで、
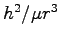 は角度方向の運動による遠心力の
効果を表わす。
適当な境界条件のもとに、これらの微分方程式を解けば解が求まる。
具体的には、まず 1 番目の式から
は角度方向の運動による遠心力の
効果を表わす。
適当な境界条件のもとに、これらの微分方程式を解けば解が求まる。
具体的には、まず 1 番目の式から 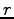 が
が 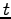 の函数として
求まり (
の函数として
求まり (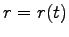 )、次にそれを 2 番目の式に代入
してまた別の微分方程式を解いて
)、次にそれを 2 番目の式に代入
してまた別の微分方程式を解いて
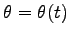 が求まる。
ここで、
が求まる。
ここで、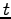 を消去すれば
を消去すれば 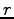 が
が 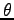 の函数として決まり、
軌道が求まることになる。ここで、角運動量の大きさ
の函数として決まり、
軌道が求まることになる。ここで、角運動量の大きさ 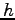 は
初期条件から決まる定数である。
は
初期条件から決まる定数である。
もし、軌道だけを求めるのであれば、Eq. (7.9) から時間微分を
消去して
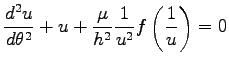 |
|
|
(0) |
という式を導くことが出来る。ここに、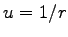 である。
万有引力
である。
万有引力
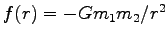 の時、これを解くと運動の
軌跡は楕円軌道 (一般には 2 次曲線) となることが分かる。
(植松、「力学」pp. 104 - 105 参照)
の時、これを解くと運動の
軌跡は楕円軌道 (一般には 2 次曲線) となることが分かる。
(植松、「力学」pp. 104 - 105 参照)
7.2 エネルギー保存則の利用 (中心力の場合の形式解)
力が保存力の時、中心力
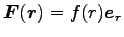 のポテンシャルは
のポテンシャルは
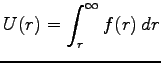 |
|
|
(0) |
で与えられるから
これを
| |
|
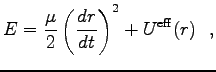 |
|
| |
|
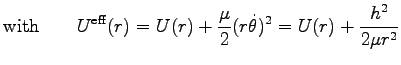 |
(0) |
と書いて、
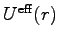 を動径部分の「有効ポテンシャル」という。
もとの
を動径部分の「有効ポテンシャル」という。
もとの 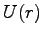 以外に、遠心力ポテンシャル
以外に、遠心力ポテンシャル
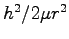 が
つけ加わっている。(
が
つけ加わっている。(
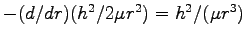 に
注意)
適当なポテンシャル
に
注意)
適当なポテンシャル 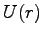 に対して、
に対して、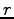 の函数として
の函数として
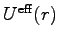 の
グラフを描くと、一般には
の
グラフを描くと、一般には 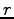 の小さい領域で遠心力の斥力が勝ち、
の小さい領域で遠心力の斥力が勝ち、
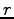 は転回点
は転回点 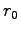 より大きいところでのみ運動が可能であることが
分かる。Eq. (7.13) から
より大きいところでのみ運動が可能であることが
分かる。Eq. (7.13) から
![$\displaystyle \frac{dr}{dt}=\pm \sqrt{\frac{2}{\mu}\left[E-U^{\rm eff}(r)\right]}$](img45.png) |
|
|
(0) |
より、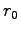 は
は
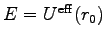 を満す (一般には、一番小さな)
を満す (一般には、一番小さな)
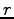 である。
である。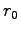 はパラメータ
はパラメータ 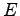 と
と 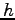 の函数である。
まず、Eq. (7.14) を
の函数である。
まず、Eq. (7.14) を 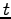 で積分すると
で積分すると
![$\displaystyle t-t_0=\pm \int^r_{r_0} \frac{dr}{\sqrt{\frac{2}{\mu}
\left[E-U^{\rm eff}(r)\right]}}$](img47.png) |
|
|
(0) |
より、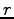 が
が 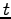 の函数として求まる。(
の函数として求まる。(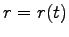 )
次に、
)
次に、
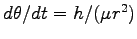 を積分して
を積分して
![$\displaystyle \theta-\theta_0=\int^t_{t_0} \frac{h}{\mu \left[r(t)\right]^2}
\,dt$](img49.png) |
|
|
(0) |
により、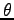 が
が 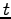 の函数として求まる。
もし、軌道だけ必要なら、
の函数として求まる。
もし、軌道だけ必要なら、
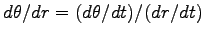 を
積分して
を
積分して
![$\displaystyle \theta-\theta_0=\pm \int^r_{r_0} \frac{\frac{h}{\mu r^2}}
{\sqrt{\frac{2}{\mu}\left[E-U(r)-\frac{h^2}{2\mu r^2}\right]}}
\,dr$](img51.png) |
|
|
(0) |
これらは、保存力、かつ中心力で相互作用する 2 質点系の相対運動の解を、
形式的にではあるが、完全に与えている。
7.3 ケプラー問題 (太陽の引力のもとでの惑星の運動)
幾つかの特別な場合には、前節の積分は解析的に求まる。
それは、ポテンシャルが万有引力ポテンシャルである場合と
調和振動子
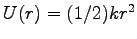 の場合である。ここでは、
前者について解を具体的に求め、ケプラーの 3 法則を導く。
簡単のため
の場合である。ここでは、
前者について解を具体的に求め、ケプラーの 3 法則を導く。
簡単のため
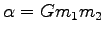 とおいて、万有引力ポテンシャルを
とおいて、万有引力ポテンシャルを
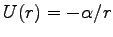 と書く。有効ポテンシャルは
と書く。有効ポテンシャルは
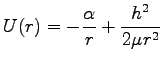 |
|
|
(0) |
で与えられる。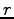 で微分して、有効ポテンシャルの極小点を
求めると
で微分して、有効ポテンシャルの極小点を
求めると
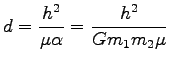 |
|
|
(0) |
が得られる。この点における有効ポテンシャルの極小値は
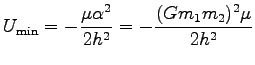 |
|
|
(0) |
である。運動可能領域が存在するためには
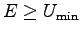 |
|
|
(0) |
でなければならない。
軌道の方程式を求めるために、最近接距離 (近日点) を 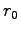 として、
として、
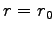 の時
の時 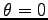 になる様に
になる様に 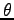 の原点を
定めると、Eq. (7.17) は
の原点を
定めると、Eq. (7.17) は
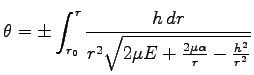 |
|
|
(0) |
となる。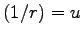 として
として 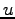 の積分へ移ると
の積分へ移ると
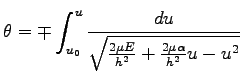 |
|
|
(0) |
ここに、ルート記号の中は、Eq. (7.19) を用いて 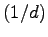 で
で
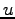 の完全平方の形に書ける。更に
の完全平方の形に書ける。更に
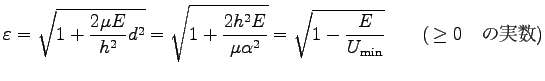 |
|
|
(0) |
と定義すると
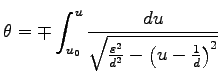 |
|
|
(0) |
この積分は、積分変数変換
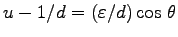 に
より、trivial となる。すなわち、
に
より、trivial となる。すなわち、
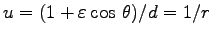 より、結局
より、結局
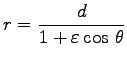 |
|
|
(0) |
この軌跡は
を表わす。
Eq. (7.27) の楕円の場合がケプラーの第 1 法則である。この時、
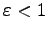 の条件から
の条件から
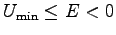 とエネルギー
とエネルギー 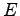 が
負の場合である事が分かる。また
が
負の場合である事が分かる。また
| |
|
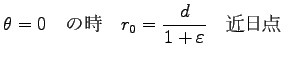 |
|
| |
|
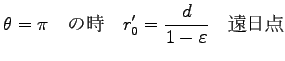 |
(0) |
また、楕円の半長径は
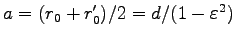 .
楕円の中心から焦点までの距離は
.
楕円の中心から焦点までの距離は
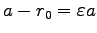 である
事が分かる。すなわち、
である
事が分かる。すなわち、
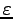 は楕円の離心率である。
楕円の半短径は
は楕円の離心率である。
楕円の半短径は
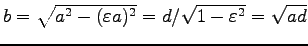 となる。
となる。
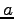 と
と 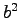 をもとの変数で書けば
をもとの変数で書けば
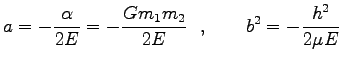 |
|
|
(0) |
すなわち、楕円の半長径は角運動量 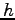 にはよらず、エネルギー
にはよらず、エネルギー 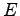 だけ
による。
ケプラーの第 2 法則は「面積速度一定」であり、それは角運動量一定に
他ならない。(中心力の性質)
だけ
による。
ケプラーの第 2 法則は「面積速度一定」であり、それは角運動量一定に
他ならない。(中心力の性質)
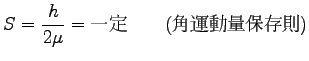 |
|
|
(0) |
ケプラーの第 3 法則を導くには、楕円の周期を 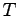 として、面積速度一定から
として、面積速度一定から
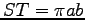 である事を用いる。ここから
である事を用いる。ここから
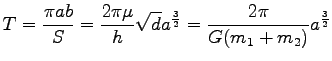 |
|
|
(0) |
が得られる。今、太陽の質量が惑星の質量に比べて十分大きいことに
注目して
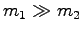 と近似すると
と近似すると
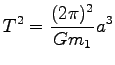 |
|
|
(0) |
となって、''公転周期の 2 乗と軌道の半長径の 3 乗の比は
惑星によらず一定'' という「ケプラーの第 3 法則」が得られる。
(参考) 2 次曲線の一般論
2 次曲線は、原点にとった1つの焦点と或る基準線との間の距離の
比が
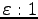 となる様な点全体の集合として特徴づけられる。
今、基準線として、直交座標表示での
となる様な点全体の集合として特徴づけられる。
今、基準線として、直交座標表示での
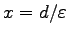 を選ぶと
この条件は Eq. (7.26) で表わされる。これを、直交座標表示すれば
(
を選ぶと
この条件は Eq. (7.26) で表わされる。これを、直交座標表示すれば
(
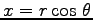 ,
,
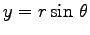 )、
)、
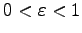 の時
の時
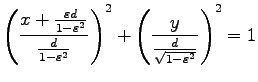 |
|
|
(0) |
となって楕円を表わすことが分かる。ここから、
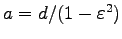 かつ
かつ
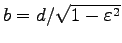 ,
,
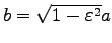 が導かれる。
また、Eq. (7.33) から、楕円の中心は
が導かれる。
また、Eq. (7.33) から、楕円の中心は
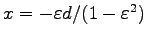 の
直線上にあり、楕円はこの軸について左右対称である事が分かる。この事は、
の
直線上にあり、楕円はこの軸について左右対称である事が分かる。この事は、
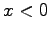 の領域にも楕円の焦点と基準線が存在することを意味し、これらに
ついても
の領域にも楕円の焦点と基準線が存在することを意味し、これらに
ついても
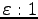 の比が成り立つ。ここから、二つの焦点から楕円上の
1 点を結んだ距離の和は
の比が成り立つ。ここから、二つの焦点から楕円上の
1 点を結んだ距離の和は 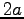 で一定であるという、楕円のよく知られた性質
が簡単に導かれる。一方、
で一定であるという、楕円のよく知られた性質
が簡単に導かれる。一方、
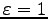 の時は、Eq. (7.26) で
表わされる曲線は放物線となり、直交表示では
の時は、Eq. (7.26) で
表わされる曲線は放物線となり、直交表示では
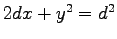 で表わされる。
更に、
で表わされる。
更に、
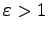 の時は、Eq. (7.26) は双曲線
の時は、Eq. (7.26) は双曲線
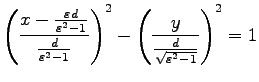 |
|
|
(0) |
となる。今度は、対称軸は
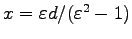 であり
平面の右側に再び同じ構造が現れる。双曲線では二つの焦点からの距離の
差が
であり
平面の右側に再び同じ構造が現れる。双曲線では二つの焦点からの距離の
差が 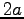 となる。
となる。
(H19.7.2 終了)



: 中心力による運動
: 物理学基礎論 A
: 質点系の運動
Yoshikazu Fujiwara
平成19年7月2日
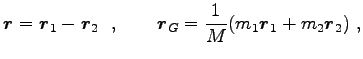
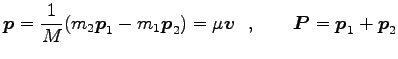
![]() ,
,
![]() として
として
![]() のポテンシャルは
のポテンシャルは
![]() の場合である。ここでは、
前者について解を具体的に求め、ケプラーの 3 法則を導く。
簡単のため
の場合である。ここでは、
前者について解を具体的に求め、ケプラーの 3 法則を導く。
簡単のため
![]() とおいて、万有引力ポテンシャルを
とおいて、万有引力ポテンシャルを
![]() と書く。有効ポテンシャルは
と書く。有効ポテンシャルは
![]() の条件から
の条件から
![]() とエネルギー
とエネルギー ![]() が
負の場合である事が分かる。また
が
負の場合である事が分かる。また
![]() となる様な点全体の集合として特徴づけられる。
今、基準線として、直交座標表示での
となる様な点全体の集合として特徴づけられる。
今、基準線として、直交座標表示での
![]() を選ぶと
この条件は Eq. (7.26) で表わされる。これを、直交座標表示すれば
(
を選ぶと
この条件は Eq. (7.26) で表わされる。これを、直交座標表示すれば
(
![]() ,
,
![]() )、
)、
![]() の時
の時